Let xandy be real variables satisfying x2+y2+8x−10y−40=0 . Let a=max{√(x+2)2+(y−3)2} and b=min{√(x+2)2+(y−3)2} . Then a+b=18 (b) a+b=√2 a−b=4√2 (d) a.b=73
a+b=18
a+b=√2
a−b=4√2
a.b=72
The correct Answer is:1,3,4
x2+y2+8x−10y−40=0
The center of the circle is (−4,5).
its radius is 9. distance of the center (−4,5) from the point (−2,3) is √4+4=2√2. Therefore, a=2√2+9 and b=−2√2+9
∴a+b=18
a−b=18
a−b=4√2
a.b=81−8=73
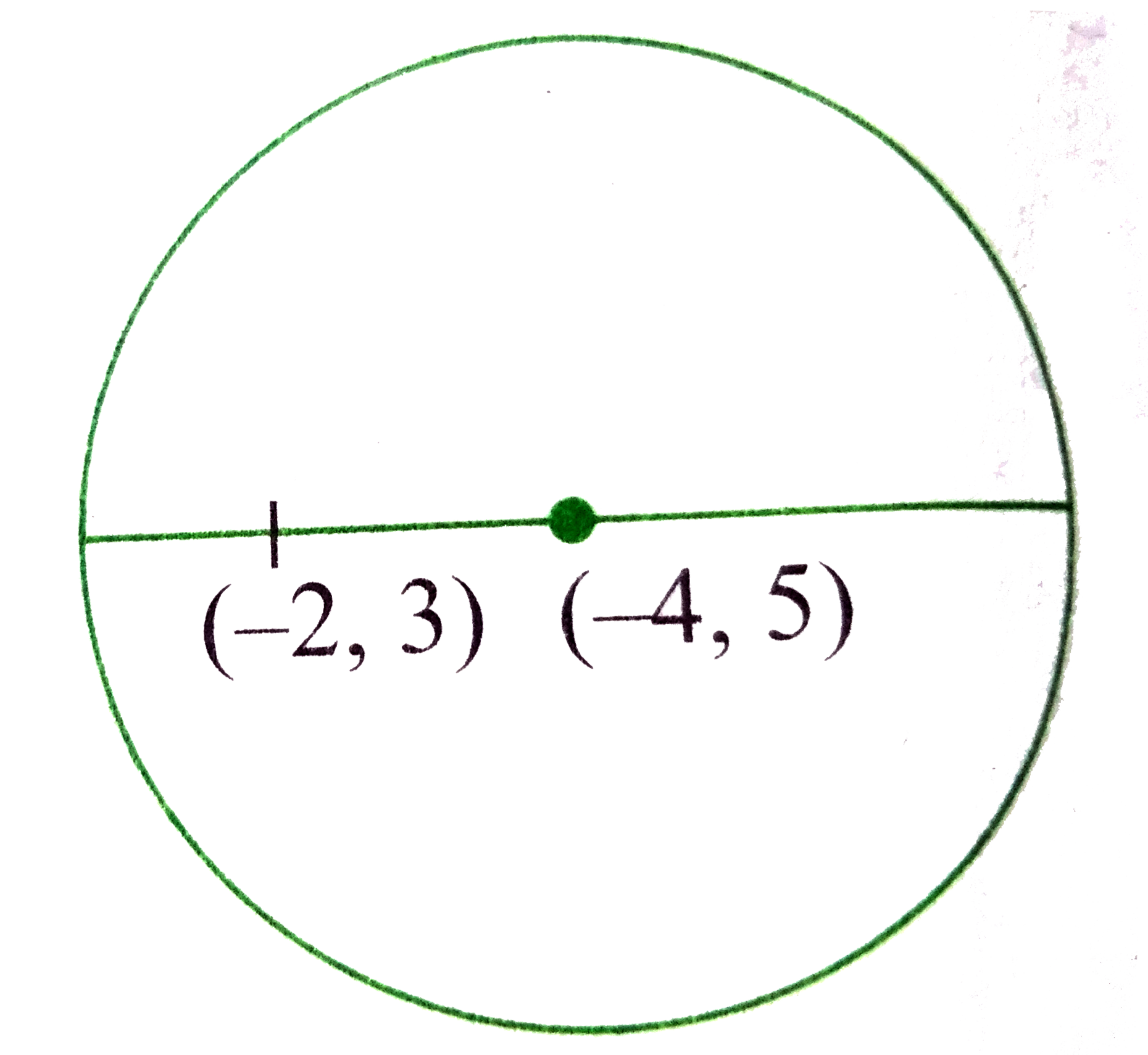
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Single)
109 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Let xandy be real variables satisfying x2+y2+8x−10y−40=0 . Let a=max{√(x+2)2+(y−3)2} and b=min{√(x+2)2+(y−3)2} . Then (a)a+b=18 (b) a+b=√2 (c) a−b=4√2 (d) a.b=73
View SolutionLet xandy be real variables satisfying x2+y2+8x−10y−40=0 . Let a=max{√(x+2)2+(y−3)2} and b=min{√(x+2)2+(y−3)2} . Then a+b=18 (b) a+b=√2 a−b=4√2 (d) a.b=73
View Solution
Knowledge Check
If a=max{(x+2)2+(y−3)2}andb=min{(x+2)2+(y−3)2} where x, y satisfying x2+y2+8x−10y−40=0 then :
Aa+b=18Ba+b=178Ca−b=4√2Da−b=72√2If 2√2x3−3√3y3=(√2x−√3y)(Ax2+by2+Cxy). Then the value of A2+B2−C2 is :
A11B10C19D7If 24√3x3+2√2y3=(2√3x+√2y)(Ax2+Bxy+Cy2), then the value of (2A+√6B−C) is:
यदि 24√3x3+2√2y3=(2√3x+√2y)(Ax2+Bxy+Cy2) है, तो (2A+√6B−C) का मान ज्ञात करें |A10B14C6D8
Let x, y be real variable satisfying x2+y2+8x−10y−59=0 Let a=max{(x−3)2+(y−4)2 and b=min{(x−3)2+(y−4)2), then a + b + 2010 is ______ .
View SolutionLet x, y be real variable satisfying x2+y2+8x−10y−59=0 Let a=max{(x−3)2+(y−4)2 and b=min{(x−3)2+(y−4)2), then a + b + 2010 is ______ .
View SolutionIf a=max{(x+2)2+(y−3)2}andb=min{(x+2)2+(y−3)2} where x, y satisfying x2+y2+8x−10y−40=0 then :
View SolutionLet S={(x,y∣(x−3)2+(y+42)2=196}
If A=min(x,y)∈S√x2+y2andB=max(x,y)∈S√x2+y2, then |B−A| is equal to
View SolutionA vertex of an equilateral triangle is at (2, 3), and th equation of the opposite side is x+y=2, then the equaiton of the other two sides are (A) y=(2+√3)(x−2),y−3=2√3(x−2) (B) y−3=(2+√3(x−2),y−3=(2−√3(x−2) (C) y+3=(2−√3(x−2),y−3=(2−√3(x+2) (D) none of these
View Solution
