Let xandy be real variables satisfying x2+y2+8x−10y−40=0 . Let a=max{√(x+2)2+(y−3)2} and b=min{√(x+2)2+(y−3)2} . Then (a)a+b=18 (b) a+b=√2 (c) a−b=4√2 (d) a.b=73Solution in Bengali
a+b=18
a+b=√2
a−b=4√2
a.b=72
The correct Answer is:1,3,4
x2+y2+8x−10y−40=0
The center of the circle is (−4,5).
its radius is 9. distance of the center (−4,5) from the point (−2,3) is √4+4=2√2. Therefore, a=2√2+9 and b=−2√2+9
∴a+b=18
a−b=18
a−b=4√2
a.b=81−8=73
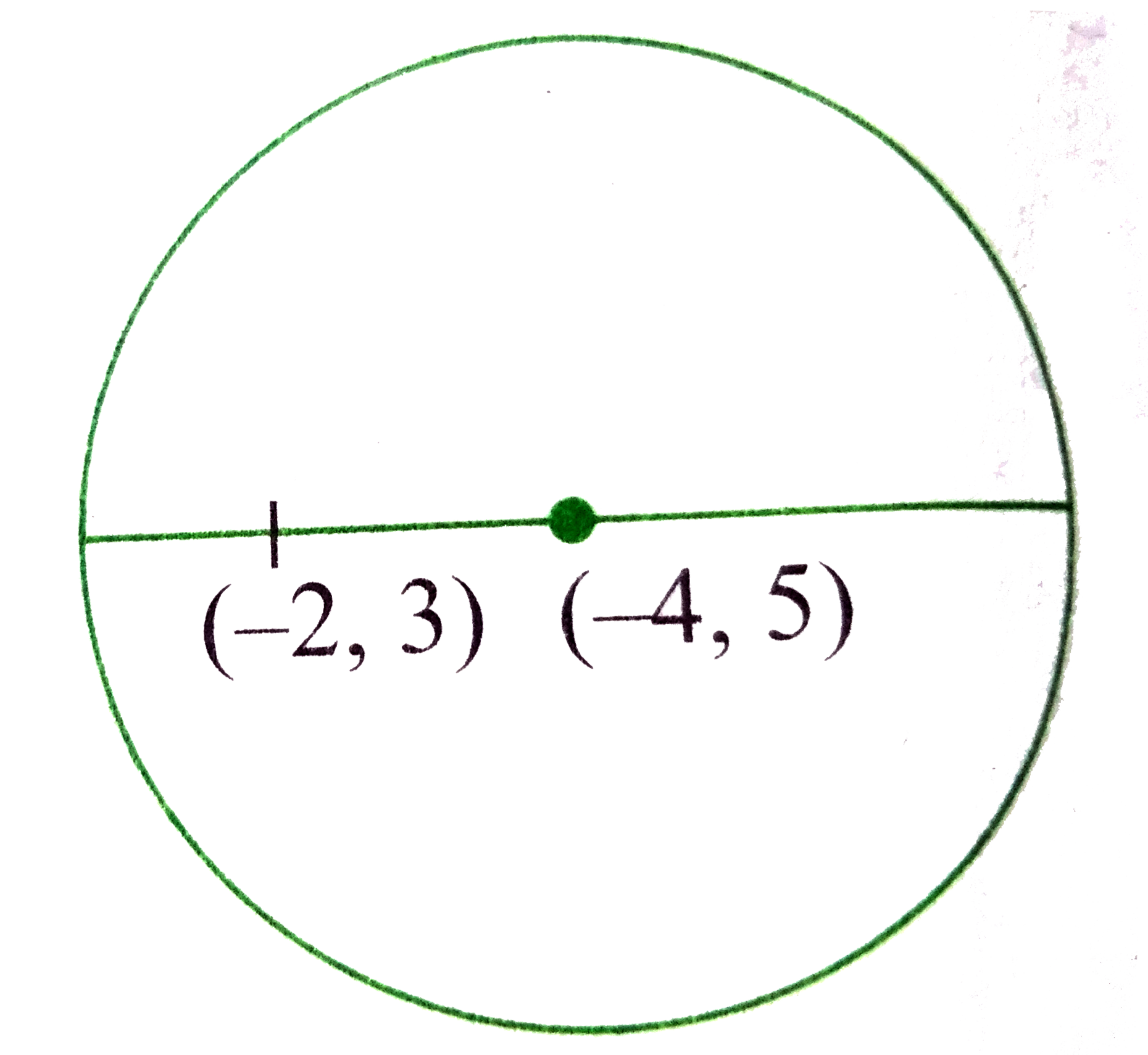
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For Problems43videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Excercises (Single Correct Answer Type)109videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Each side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
07:08View SolutionTangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?04:13View SolutionThe number of rational point(s) [a point (a, b) is called rational, if aandb both are rational numbers] on the circumference of a circle having center (π,e) is at most one (b) at least two exactly two (d) infinite
04:30View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is09:30View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is05:11View SolutionLet a,b,xandy be real numbers such that a−b=1andy≠0. If the complex number z=x+iy satisfies Im(az+bz+1)=y , then which of the following is (are) possible value9s) of x? (a)−1−√1−y2 (b) 1+√1+y2 (c)−1+√1−y2 (d) −1−√1+y2
03:09View SolutionLet xandy be real variables satisfying x2+y2+8x−10y−40=0 . Let a=max{√(x+2)2+(y−3)2} and b=min{√(x+2)2+(y−3)2} . Then a+b=18 (b) a+b=√2 a−b=4√2 (d) a.b=73
02:55View SolutionLet a solution y = y(x) of the differential equation x√x2−1dy−y√y2−1dx=0, satisfy y(2)=2√3
03:37View SolutionLet x, y be real variable satisfying x2+y2+8x−10y−59=0 Let a=max{(x−3)2+(y−4)2 and b=min{(x−3)2+(y−4)2), then a + b + 2010 is ______ .
02:29View SolutionIf a=max{(x+2)2+(y−3)2}andb=min{(x+2)2+(y−3)2} where x, y satisfying x2+y2+8x−10y−40=0 then :
02:56View SolutionLet S={(x,y∣(x−3)2+(y+42)2=196}
If A=min(x,y)∈S√x2+y2andB=max(x,y)∈S√x2+y2, then |B−A| is equal to03:43View SolutionIf y=(x+√x2+a2)n,thendydx is (a)ny√x2+a2 (b) −ny√x2+a2 (c)nx√x2+a2 (d) −nx√x2+a2
05:21View SolutionLet xandy be real variables satisfying x2+y2+8x−10y−40=0 . Let a=max{√(x+2)2+(y−3)2} and b=min{√(x+2)2+(y−3)2} . Then (a)a+b=18 (b) a+b=√2 (c) a−b=4√2 (d) a.b=73
02:21View SolutionIf y=(x+√x2+a2)n,thendydx is ny√x2+a2 (b) −ny√x2+a2 nx√x2+a2 (d) −nx√x2+a2
04:24View SolutionIf y=(x+√x2+a2)n,thendydx is ny√x2+a2 (b) −ny√x2+a2 nx√x2+a2 (d) −nx√x2+a2
02:42View SolutionLet a,b,xandy be real numbers such that a−b=1andy≠0. If the complex number z=x+iy satisfies Im(az+bz+1)=y , then which of the following is (are) possible value9s) of x?| −1−√1−y2 (b) 1+√1+y2 −1+√1−y2 (d) −1−√1+y2
05:19View Solution

