lf from point P(4,4) perpendiculars to the straight lines 3x+4y+5=0 and y=mx+7 meet at Q and R area of triangle PQR is maximum, then m is equal to
The correct Answer is:4
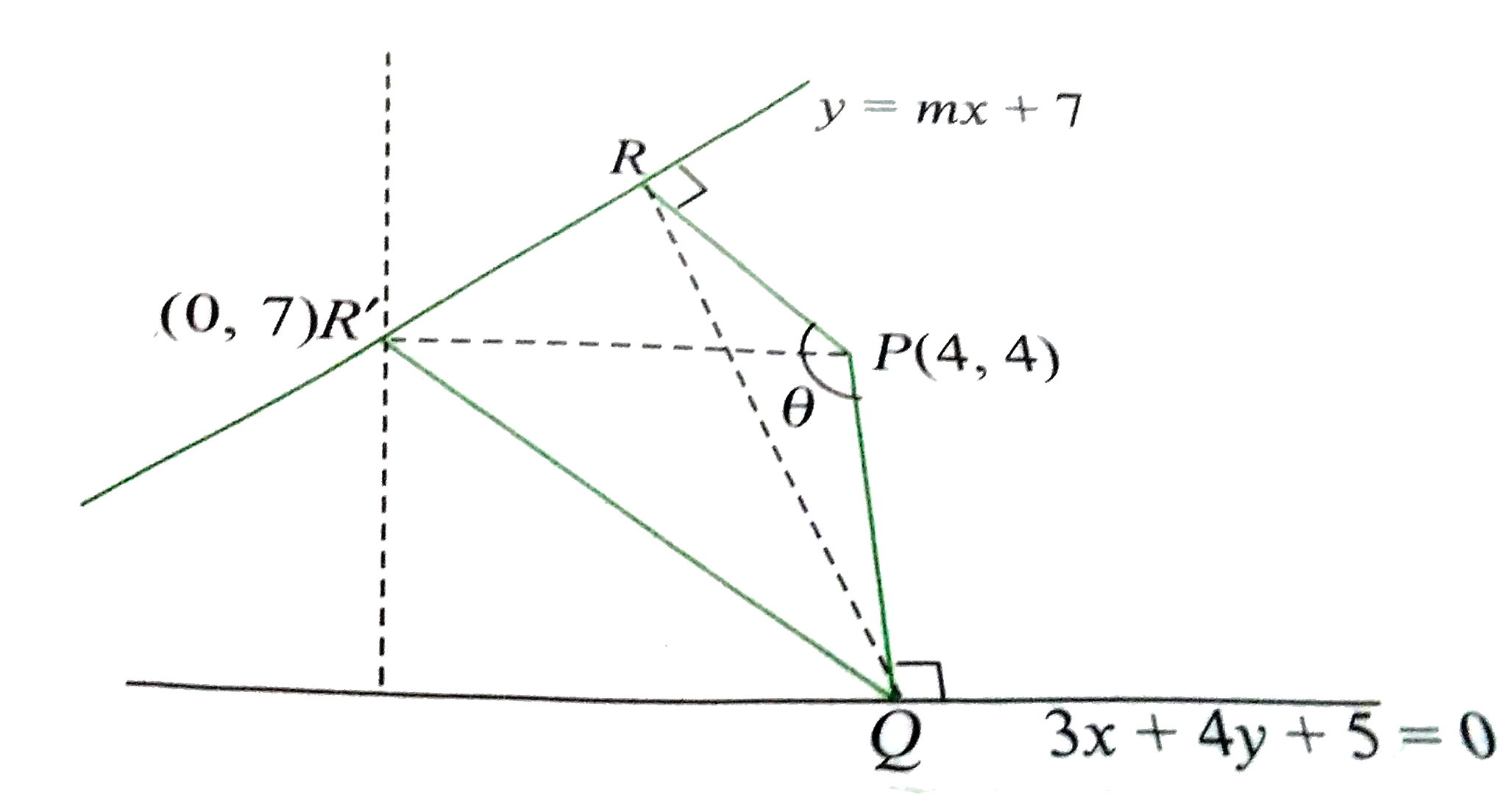
Since PQ is of fixed length,
Area of ΔPQR=12|PQ||RP|sinθ
This will be maximum if sinθ=1 and RP is maximum .
Since y=mx+7 passes through R'(0,7) it must be rotated about (0,7) such that in new position, θ becomes 90∘ i.e., the line becomes perpendicular to 3x+4y+5=0, then the slope of line 43.
That is of PR'=4−74−0=−34 = slope of given line. That is the in new position of the line. R coincides with R'.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
lf from point P(4,4) perpendiculars to the straight lines 3x+4y+5=0 and y=mx+7 meet at Q and R area of triangle PQR is maximum, then m is equal to
View SolutionFrom a pointP=(3,4) perpendiculars PQ and PR are drawn to line 3x+4y−7=0 and a variable line y−1=m(x−7) respectively then maximum area of triangle PQR is :
View Solution
Knowledge Check
Area of triangle formed by straight lines 3x−4y=0,x=4 and x-axis
A6 sq. unitB8 sq. unitC12 sq. unitD16 sq. unitArea of triangle formed by straight lines 3x−y=3,x−2y+4=0andy=0 is
A154 sq. unitB152 sq. unitC15 sq. unitDCannot be determinedConsider the parabola y2=4x, let P and Q be two points (4,−4) and (9,6) on the parabola. Let R be a moving point on the arc of the parabola whose x-coordinate is between P and Q. If the maximum area of triangle PQR is K, then (4K)1/3 is equal to
A1B2C5D7
From a pointP=(3,4) perpendiculars PQ and PR are drawn to line 3x+4y−7=0 and a variable line y−1=m(x−7) respectively then maximum area of triangle PQR is :
View Solutionif P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
View Solutionif P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
View SolutionFrom the point (3 0) 3- normals are drawn to the parabola y2=4x. Feet of these normal are P ,Q ,R then area of triangle PQR is
View SolutionConsider a point P(4,√2) points Q,R which respectively lie on the lines y=x y=0. If ΔPQR is formed and its minimum perimeter is a, then a is equal to
View Solution
