(lim)x→1nxn+1−(n+1)xn+1(ex−e)sinπx, wheren=100, is equal to : 5050πe (b) 100πe (c) −5050πe (d) −4950πeSolution in Punjabi
5050πe
100πe
−5050πe
−4950πe
The correct Answer is:A
Step by step video solution for ("lim")_(xto1)(n x^(n+1)-(n+1)x^n+1)/((e^x-e)sinpix),\ where \n=100 , is equal to : (5050)/(pie) (b) (100)/(pie) (c) -(5050)/(pie) (d) -(4950)/(pie) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES
1 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
38 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
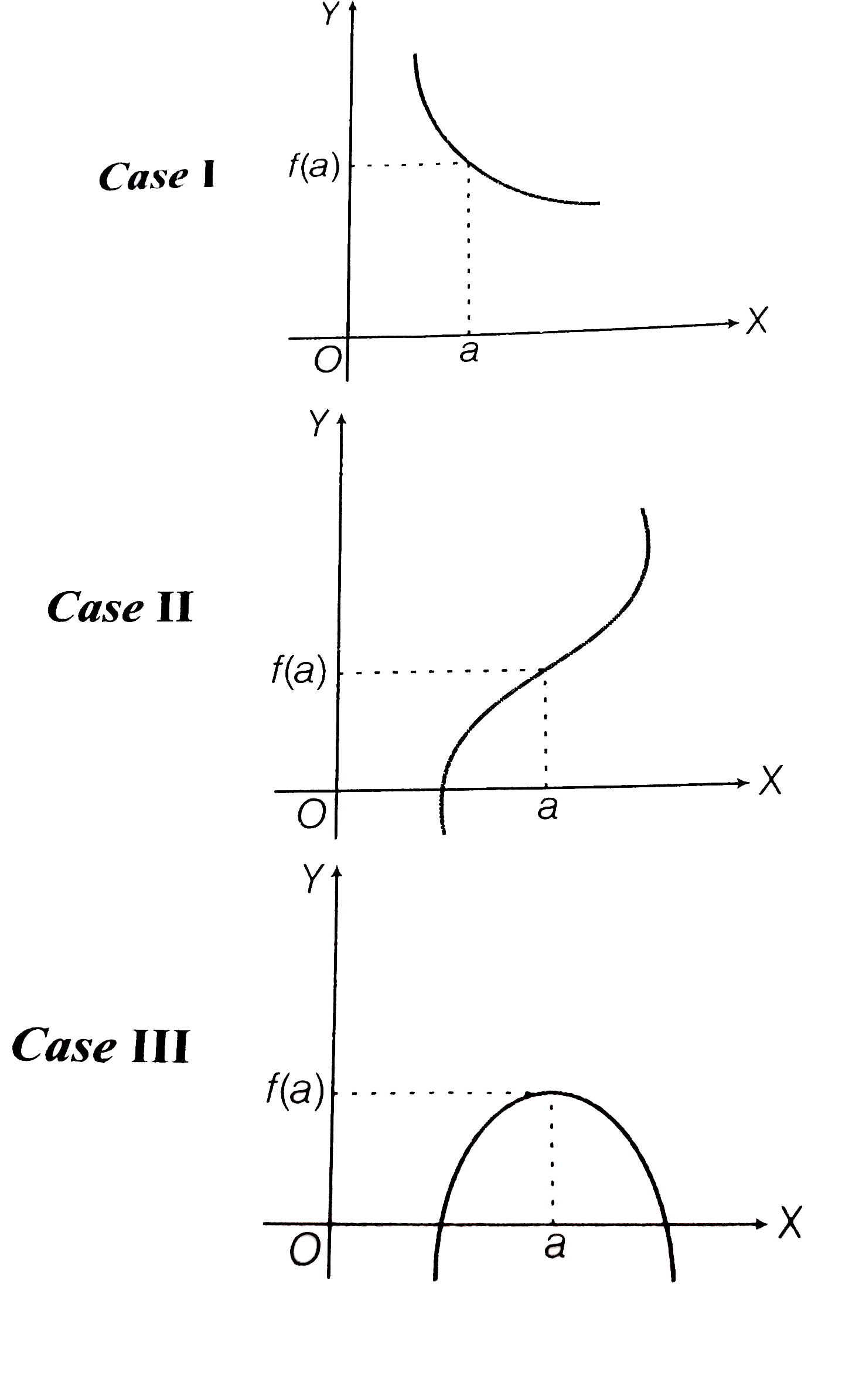
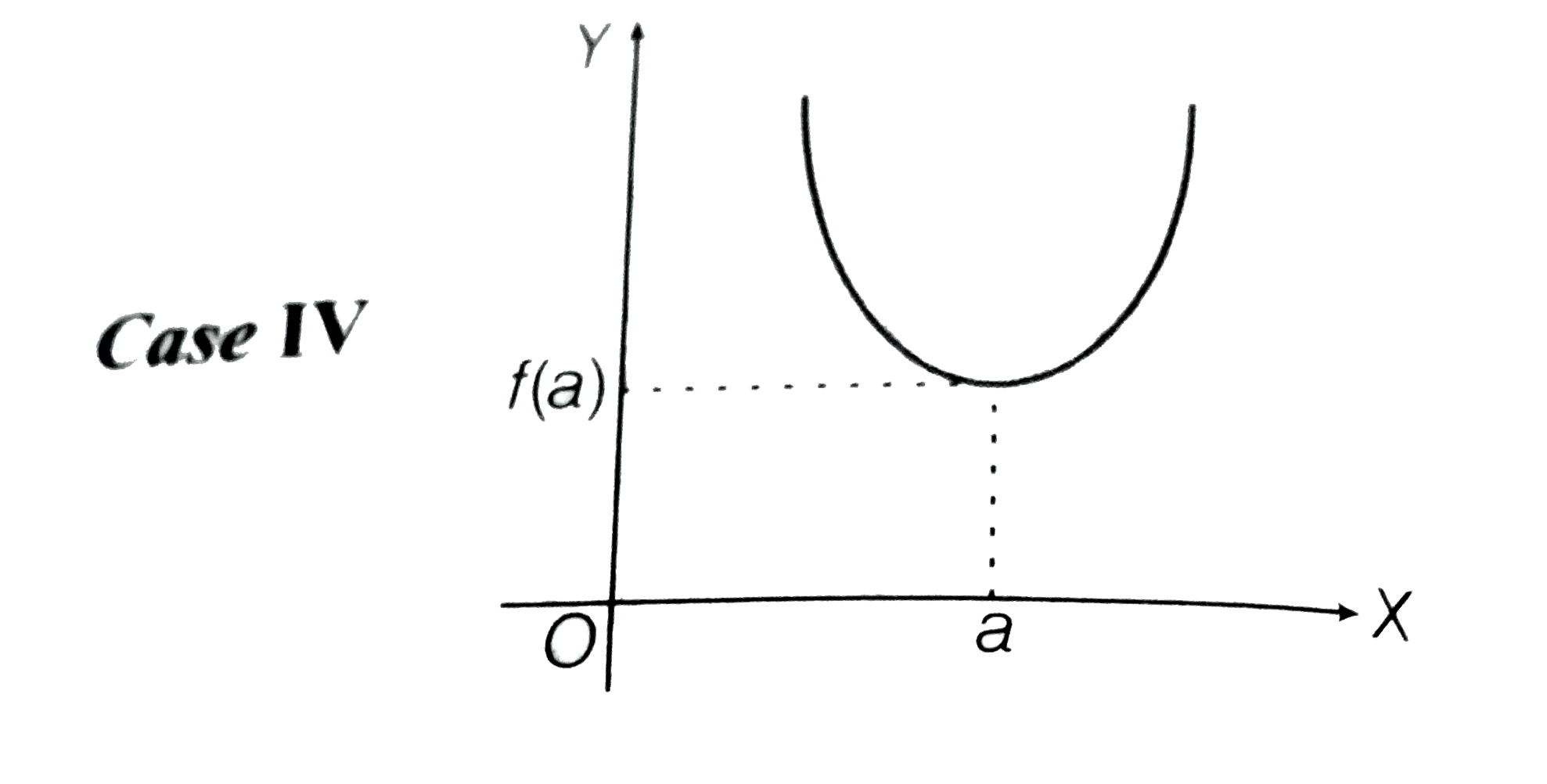
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View Solutionlimx→0sin(πcos2(tan(sinx)))x2 is equal to
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View Solution(lim)x→1nxn+1−(n+1)xn+1(ex−e)sinπx,wheren=100, is equal to : 5050πe (b) 100πe (c) −5050πe (d) −4950πe
View SolutionIf A(n) represents the area bounded by the curve y=n⋅lnx ,where n∈Nandn>1, the x-axis and the lines x=1andx=e, then the value of A(n)+nA(n−1) is equal to a.n2e+1 b. n2e−1 c. n2 d. en2
View SolutionIf f(x)=100∏n=1(x−n)n(101−n),wherek∏i=1ai stands for product a1.a2.........ak, then f(101)f′(101)= (a)5050 (b) 15050 (c) 10010 (d) 110010
View Solutionf(x)=(e^(x))/(e^(x)+sqrt(e)), the sum_(N=1)^(1-100)f'(N)-f'(1-N) is equal to,when N in Natural number
View Solution(lim)x→0(1x+2x+3x++nxn)1x is equal to (n !) n b. (n!)1/n c. n! d. ln(n!)
View SolutionIf the coefficient of x100 isn 1+(1+x)+1+x)2+(1+x)3+………+(1+x)n,(n.−100)is201C101 then n= (A) 100 (B) 200 (C) 101 (D) none of these
View SolutionIf limx→1x+x2+x3+....+xn−nx−1=5050 , then n=
View SolutionIf limx→1x1+x2+x3+...+xn−nx−1=820,(n∈N)
then the value of n is equal to
View Solution(lim)x→1nxn+1−(n+1)xn+1(ex−e)sinπx, where n=100, is equal to :
View SolutionIfIn=∫π0ex(sinx)ndx,thenI3I1is equal to 35 (b) 15 (c) 1 (d) 25
View SolutionThe value of limx→∞(2xn)e1x−(3xn)e1xxn (where n∈N) is
View Solutionlimx→1nxn−1−(n+1)xn+1(ex−e)sinπx, where n=100,is equal to
View Solution
