Line L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then a2+b2=p2+q2 1a2+1b2=1p2+1q2 a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
a2+b2=p2+q2
1a2+1b2=1p2+1q2
a2+p2=b2+q2
1a2+1p2=1b2+1q2
The correct Answer is:B
The equation of line L with reference to the old axis is
xa+yb=
OM=Length of the perpendicular from O(0,0) on it
⇒OM=1√1a2+1b2 …(i)
Let the axes be rotated through an angle θ . With reference to the new axes, the equation of the line L is
xp+yq=1
∴ OM =Length of hte perpendicular from O(0,0) on it
⇒Om=1√1p2+1q2 ...(ii)
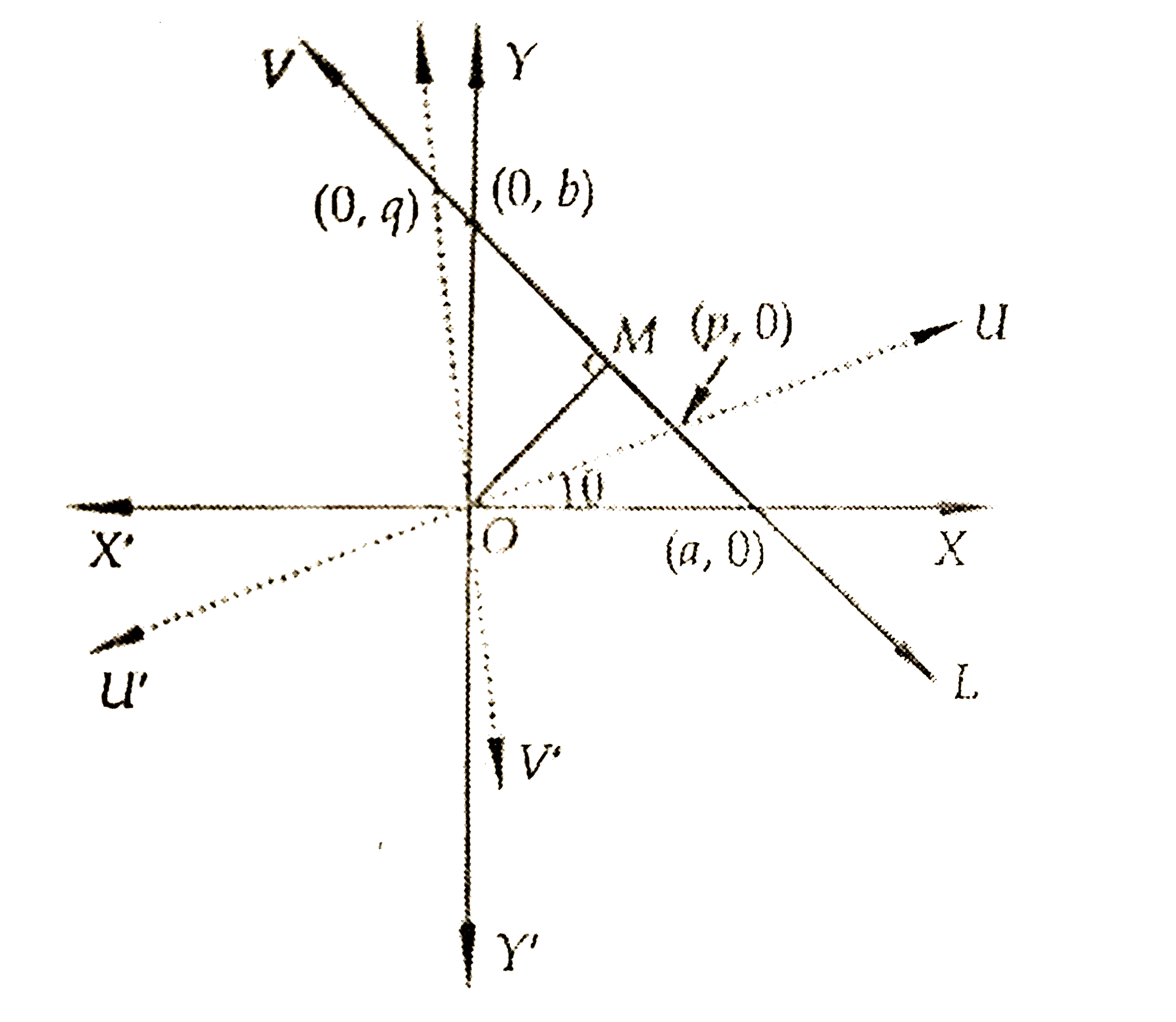
From (i) and (ii), we get
2√1a2+1b2=1√1p2+1q2⇒1a2+1b2=1p2+1q2
This is the required relation .
ALITER The equation of the line with reference to the old axes is xa+yb=1 ...(i)
If the axes are rotated through an angle θ, then
x=Xcosθ−Ysinθ,y=Xsinθ+Ycosθ
here X and Y coordinates of a point P(x,y) with respect to new-axes
The equation of the line with respect to new axes is
Xp+Yq=1 (ii)
Substituting the values of x and y in (i) , we get
(cosθa+sinθb)X+(−sinθa+cosθb)Y=1 ...(iii)
Clearly, (ii) and (iii) represent the same line . Therefore,
1p=cosθa+sinθband,1q=−sinθa+cosθb
⇒1p2+1q2=1a2+1b2, which is the required relation.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section I - Solved Mcqs
64 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
Line L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then (a) a2+b2=p2+q2 (b)1a2+1b2=1p2+1q2 (c)a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
View SolutionLine L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then (a) a2+b2=p2+q2 (b)1a2+1b2=1p2+1q2 (c)a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1p2=1a2+1b2.
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1p2=1a2+1b2 .
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1p2=1a2+1b2.
View SolutionIf p is the perpendicualr distance of the origin from the line whose intercepts on the axes are a and b, show that
1p2=1a2+1b2
View SolutionIf p be the length of the perpendicular from the origin on the line x/a+y/b =1, then p2=a2+b2 b. p2=1a2+1b2 c. 1p2=1a2+1b2 d. none of these
View SolutionIf a plane has intercepts a, b and c on the coordinate axes and is at a distance of p units from the origin, prove that they 1a2+1b2+1c2=1p2
View SolutionProve that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then 1a2+1b2+1c2=1p2.
View SolutionGiven that tanα and tanβ,x2−px+q=0 , then value of sin2(α+β)= p2p2+(1−q)2 (b) p2p2+q2 q2p2+(1−q)2 (d) p2(p+q)2
View Solution
