Lists I, II and III contains conics, equation of tangents to the conics and points of contact, respectively.

If the tangent to a suitable conic (List I) at (√312) is found to be √3x+2y=4. then which of the following options is the only CORRECT combination?
(II) (iii) (R)
(IV) (iv) (S)
(IV) (iii) (S)
(II) (iv) (R)
The correct Answer is:D
Tangent is (√3,12) is
√3x+2y=4
Since slope of tangent at (√3,12) is −ve, possible curves are (I) and (II) only (draw the diagram and verify).
Also, given equation of tangent cannot match with
my=x2x+a.
So, comparing eq. (I) with y=mx+a√x2+1, we get
a=2 and m=−√32.
Therefore, equation of curve is x24+y=1.
The corresponding point of contact is
(−a2m√a2m2+1,1√a2m2+1)
Topper's Solved these Questions
Similar Questions
Matching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
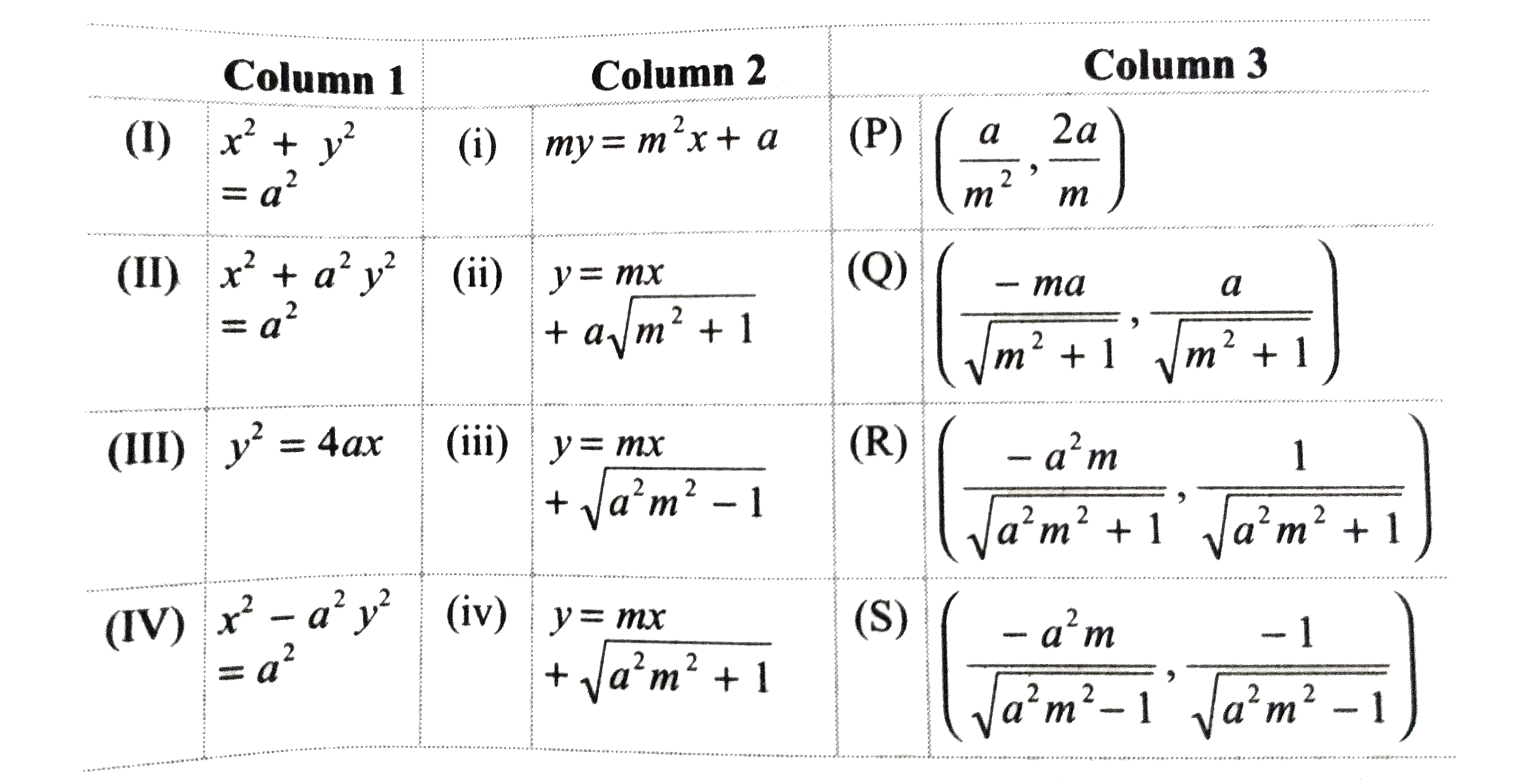
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
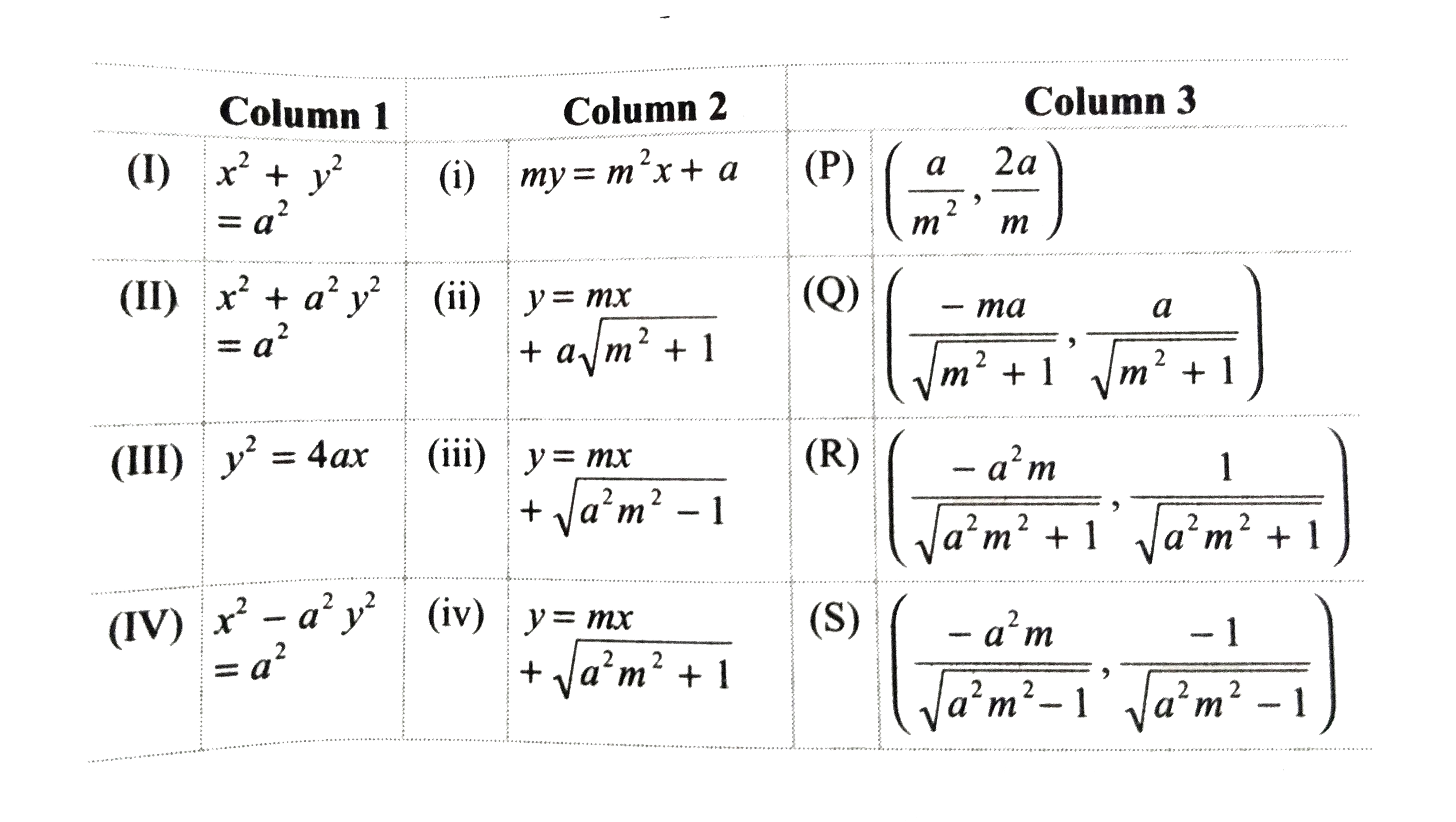
Q. For a=√2), if a tangent is drawn to a suitable conic (Column 1) at the points of contact (-1, 1), then which of the following options is the only correct combination for obtaining its equation?
View Solution
Knowledge Check
Lists I, II and III contains conics, equation of tangents to the conics and points of contact, respectively.

If a tangent to a suitable conic (List I) is fond to be y = x+8 and its point of contact is (8, 16), then which of the following options I sthe only CORRECT combination?A(II) (i) (P)B(III) (i0) (Q)C(II) (iv) (R)D(I) (ii) (Q)Lists I, II and III contains conics, equation of tangents to the conics and points of contact, respectively.

For a=√2 if a tangent is drawn to a suitable conic (List I) at the point of contact (−1,1), which of the following options is the only CORRECT combination for obtaining its equation?A(II) (ii) (Q)B(III) (i) (P)C(I) (i) (P)D(I) (ii) (Q)
Column 1,2 and 3 contains conics, equations of tangents to the conics and points of contact, respectively. Column I, Column 2, Column 3 I, x2+y2=a , (i), my=m2x+a , (P), (am2,2am) II, x2+a2y2=a , (ii), y=mx+a√m2+1 , (Q), (−ma√m2+1,a√m2+1) III, y2=4ax , (iii), y=mx+√a2m2−1 , (R), (−a2m√a2m2+1,1√a2m2+1) IV, x2−a2y2=a2 , (iv), y=mx+√a2m2+1 , (S), (−a2m√a2m2+1,−1√a2m2+1) The tangent to a suitable conic (Column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the only CORRECT combination? (IV) (iii) (S) (b) (II) (iii) (R) (II) (iv) (R) (d) (IV) (iv) (S)
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1)
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1).
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1)
View SolutionA common tangent to the conics x2=6yand2x2−4y2=9 is
View SolutionColumn 1,2 and 3 contains conics, equations of tangents to the conics and points of contact, respectively. Column I, Column 2, Column 3 I, x2+y2=a , (i), my=m2x+a , (P), (am2,2am) II, x2+a2y2=a , (ii), y=mx+a√m2+1 , (Q), (−ma√m2+1,a√m2+1) III, y2=4ax , (iii), y=mx+√a2m2−1 , (R), (−a2m√a2m2+1,1√a2m2+1) IV, x2−a2y2=a2 , (iv), y=mx+√a2m2+1 , (S), (−a2m√a2m2+1,−1√a2m2+1) If a tangent to a suitable conic (Column 1) is found to be y=x+8 and its point of contact is (8,16), then which of the followingoptions is the only CORRECT combination? (III) (ii) (Q) (b) (II) (iv) (R) (I) (ii) (Q) (d) (III) (i) (P)
View Solution
