Locataed in Nigdi, the Bhakti Shakti flag was set up by the PCMC in 2018. The approximately 105 metre high flagpole and the flag is made up of knitted polyester. The height of the flagpole is PQ and the distance between the foot of the flagpole Q and a point R on the ground is 208m.

The value of tan2P−sec2P is
0
1
−1
2
Step by step video & image solution for Locataed in Nigdi, the Bhakti Shakti flag was set up by the PCMC in 2018. The approximately 105 metre high flagpole and the flag is made up of knitted polyester. The height of the flagpole is PQ and the distance between the foot of the flagpole Q and a point R on the ground is 208m. The value of tan^(2)P- sec^(2)P is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section -B
20 Videos
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C
10 Videos
- SAMPLE PAPER 10 SOLVED BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 SOLVED EXERCISE - PART - B (SECTION - V)
4 Videos
Similar Questions
Locataed in Nigdi, the Bhakti Shakti flag was set up by the PCMC in 2018. The approximately 105 metre high flagpole and the flag is made up of knitted polyester. The height of the flagpole is PQ and the distance between the foot of the flagpole Q and a point R on the ground is 208m.

The value of sin P is
View SolutionLocataed in Nigdi, the Bhakti Shakti flag was set up by the PCMC in 2018. The approximately 105 metre high flagpole and the flag is made up of knitted polyester. The height of the flagpole is PQ and the distance between the foot of the flagpole Q and a point R on the ground is 208m.

The value of cosecR is
View Solution
Knowledge Check
When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−2m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?A2×10−3Pa−sB1×10−3Pa−sC4×10−3Pa−sD5×10−4Pa−sIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Intensity at point Q when screen is at position (1) is
 A0.5 I0B5I0CzeroDnone of these
A0.5 I0B5I0CzeroDnone of these
Locataed in Nigdi, the Bhakti Shakti flag was set up by the PCMC in 2018. The approximately 105 metre high flagpole and the flag is made up of knitted polyester. The height of the flagpole is PQ and the distance between the foot of the flagpole Q and a point R on the ground is 208m.

tanP−cotR is
View SolutionLocataed in Nigdi, the Bhakti Shakti flag was set up by the Pimpri Chinchwad Municipal Corporation (PCMC) in 2018. The approximately 105 metre high flagpole weighs 42 tonnes and the flag is made up of knitted polyester and the flag itself weighs 90kg and can sustain winds up to 25km per hour. The height of the flag is shown in the picture as PQ and the distance between the foot of the flagpole Q and a point R on the ground is 208m.
The value of cos R is
View SolutionThe circuit diagram given in the figure shown the experimental setup for the measurement of unknown resistance by using a metre bridge. The wire connected between the points P and Q(PQ = 100 cm) has uniform cross-sectional area and its resistivity is directly proportional to the distance from point P. Null point is obtained with the jockey J with R1andR2 in the gaps. If R1andR2 are interchanged, the jockey has to be displaced through a distance from the previous position along the wire to establish the null point. If the ratio of R1R2=3 , the value of Δ (in cm) is: [Ignore any end corrections]

View SolutionA vessel ABCD of 10cm width has two small slits S1 and S2 sealed with idebtical glass plates of equal thickness. The distance between the slits is 0.8mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S,40cm below P and 2m from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line OQ. Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

View SolutionTwo long parallel wires carrying current 2.5amperes and Iampere in the same direction ( directed into the plane of the paper) are held at PandQ respectively such that they are perpendicular to the plane of paper. The points PandQ are located at a distance of 5metresand2metres respectively from a collinear point R ( see figure)
(i) An electron moving with a velocity of 4×105m/s along the positive x−direction experiences a force of magnitude 3.2×10−20N at the point R. Find the value of I.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude 2.5amperes may be placed so that the magnetic induction at R is zero.
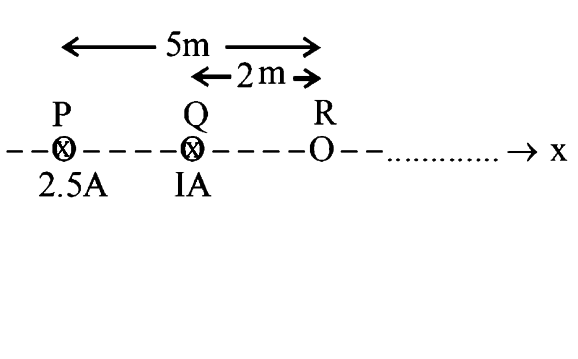
View SolutionA vessel ABCD of 10 cm width has two small slits s1 and S2 sealed, with identical glass plates of equal thickness. The distance between the slits is 0.8. mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept al S. 40 cm below P and 2m from the vessel, to illuminate the slits as shown in the figure below. 40cm Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled up to-OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid

View Solution
