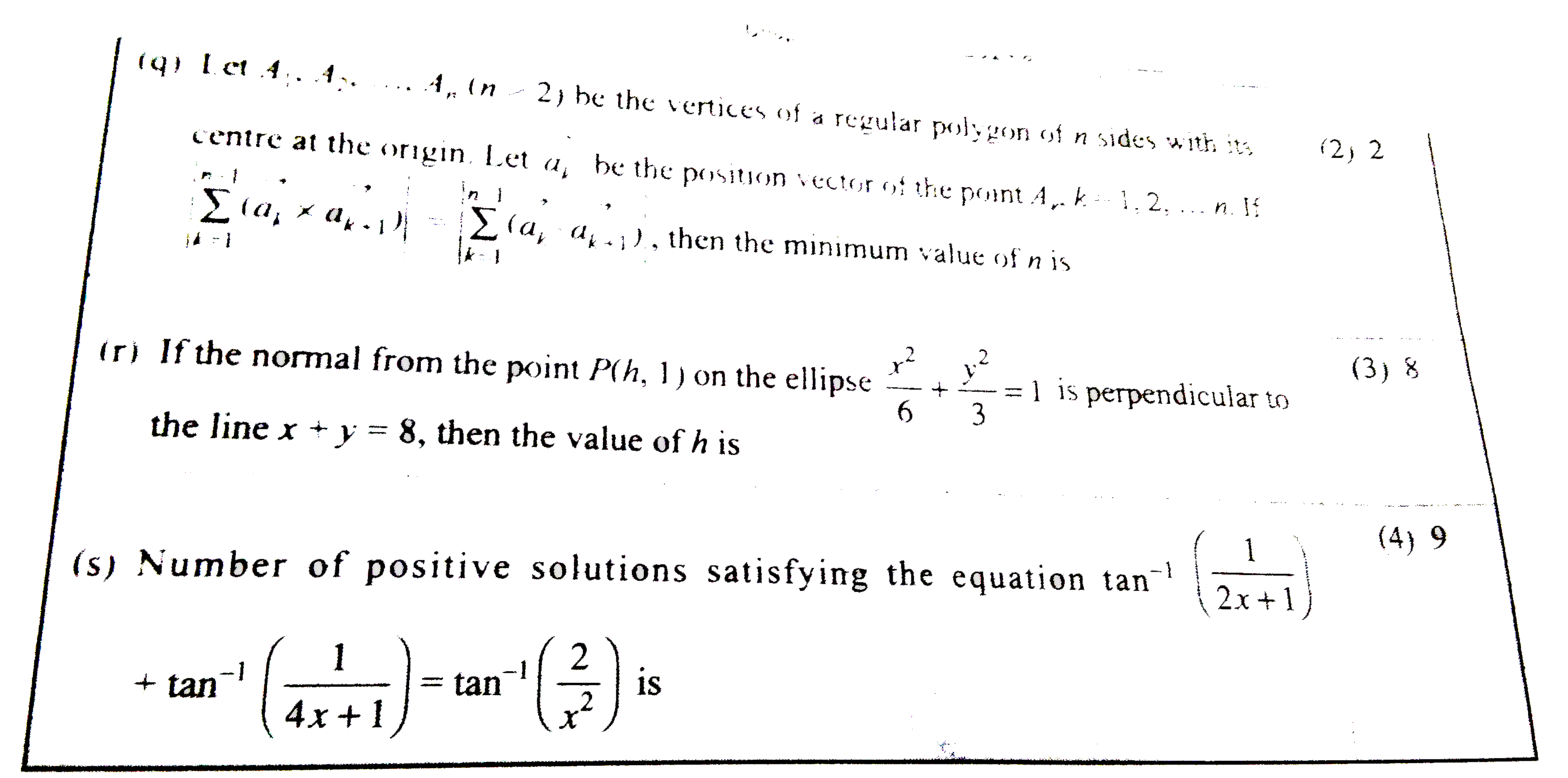(p)(q)(r)(s)(4)(3)(2)(1)
(p)(q)(r)(s)(2)(4)(3)(1)
(p)(q)(r)(s)(4)(3)(1)(2)
(p)(q)(r)(s)(2)(4)(1)(3)
The correct Answer is:A
q.(→ak×→ak+1)=r2sin2πn
→ak.→aK+1=r2cos2πn
Given∣∣
∣∣n−1∑k−1→ak×→ak+1∣∣
∣∣=∣∣
∣∣n−1∑k=1ak.ak+1∣∣
∣∣
⇒r2(n−1)sin2πn=r2(n−1)cos2πn
⇒tan2πn=1
⇒tan(2π)n=kπ+π4,K∈Z
⇒84K+1
⇒n=8 ( when=0)
Note :- Solutions of the remaining pats are given in their respective chapters.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - chapter -3 multiple correct answers type2videos
JEE 2019
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - chapter-21videos
JEE 2019
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - chapter -2 multiple correct answers type2videos
JEE 2019
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions529videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Question Bank17videos
LIMITS
Similar Questions
let L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1:x+2y−z+1=0 and P2:2x−y+z−1=0, Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie(s) on M?
01:37View SolutionLet →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is correct ?
06:07View SolutionLet →x,→yand→z be three vector each of magnitude √2 and the angle between each pair of them is π3. if →a is a non - zero vector perpendicular to →xand→y×→zand→b is a non-zero vector perpendicular to →yand→z×→x, then
02:11View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
01:31View SolutionIf Limx→01−cosxeax−bx−1 exist and is equal to 1, then (a2+b2) equals
02:45View SolutionHow many lines of symmetry does the above figure have ?
02:17View SolutionWhich of the following are correct chain isomers of butane ? (i)
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
02:21View SolutionDtermine the images of the following figure about the given line :
02:03View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionFind the area of the figure given below.
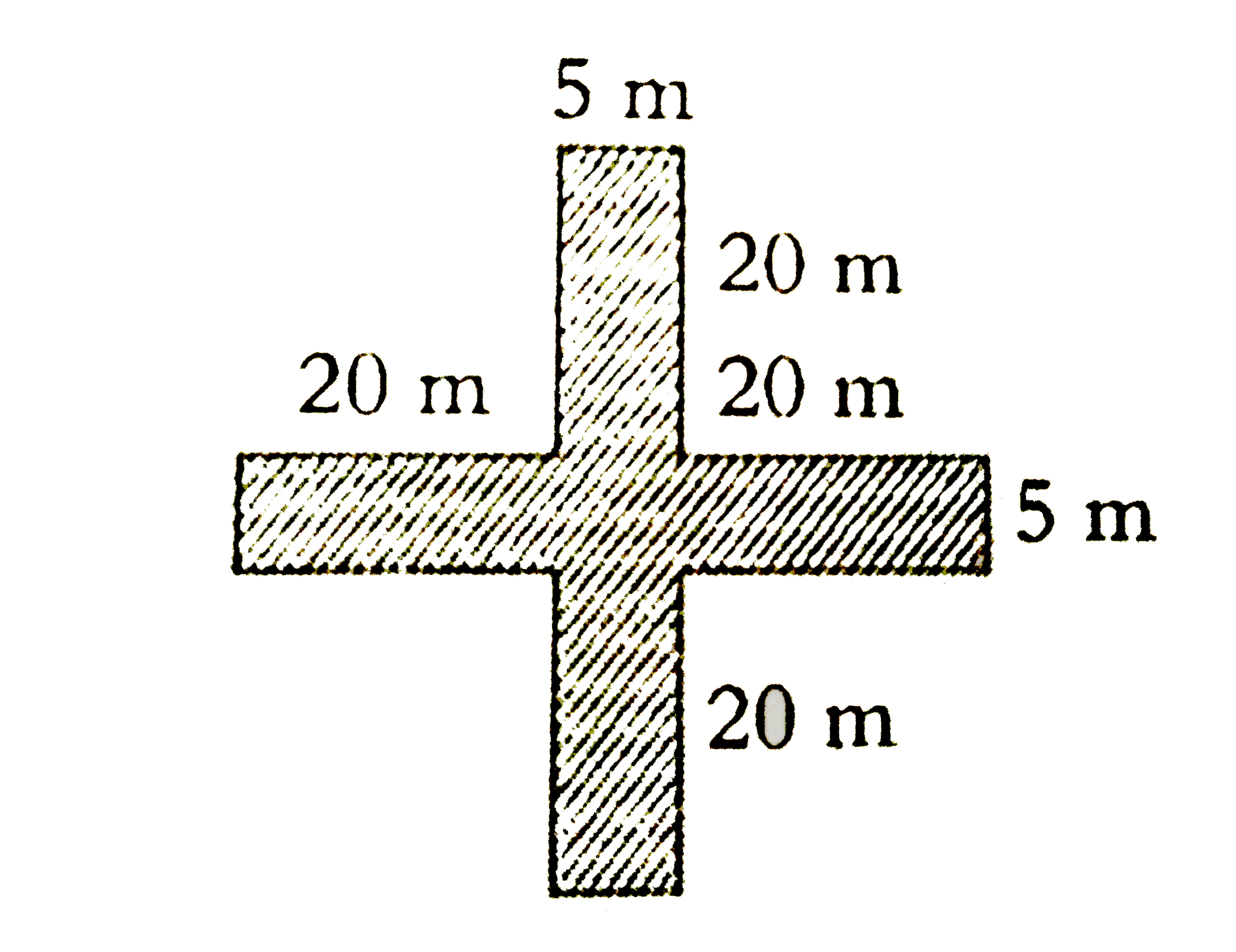 04:23View Solution
04:23View SolutionThe area of the shaded part in the figure given below is ______.
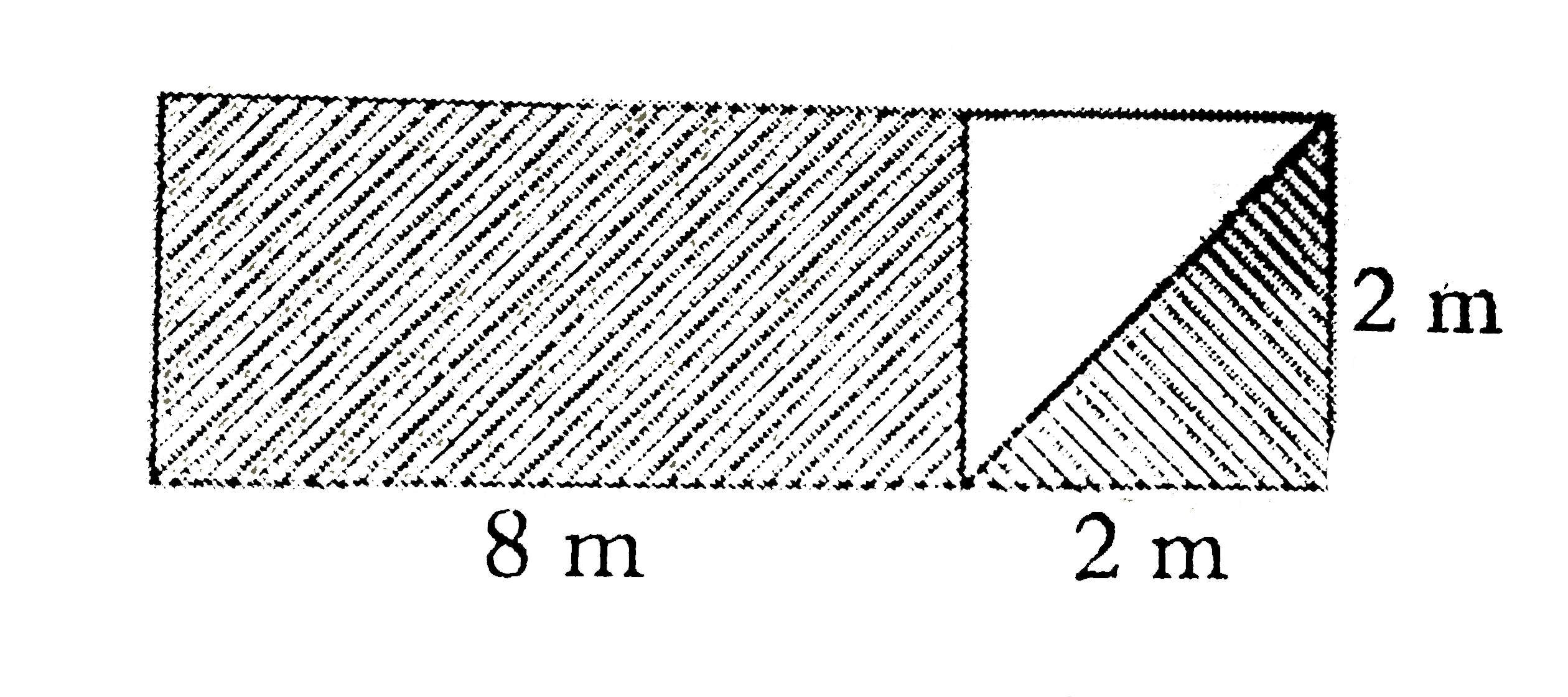 01:13View Solution
01:13View SolutionThe inequation represented by the graph given below is :
03:12View SolutionThe inequation that best describes the graph given below is _________
05:46View Solution