is the foot of the perpendicular from a point on a parabola to its directrix and is an equilateral triangle, where S is the focus. Then find .Solution in Tamil
This given fixed point is .
From given fig.,
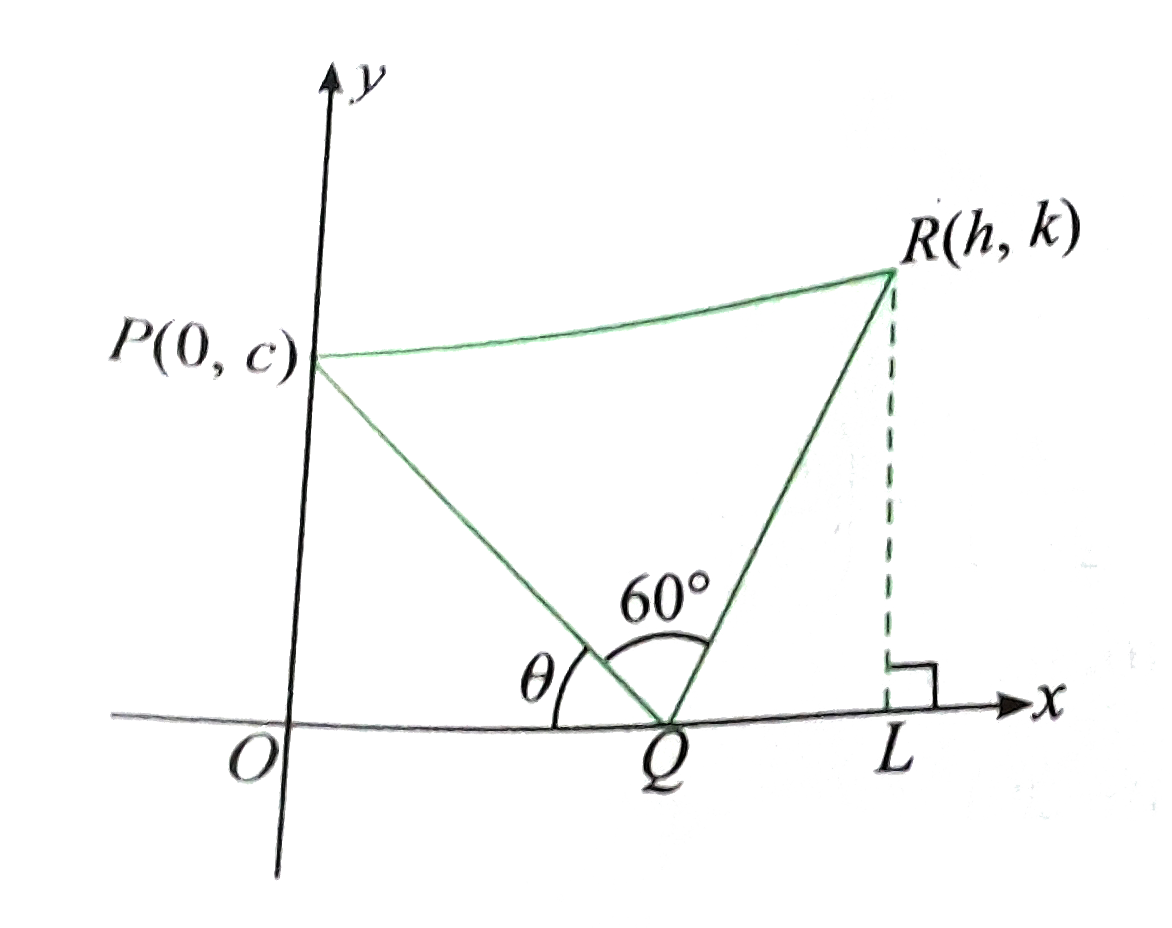
(1)
Now,
Eliminating from (1) and (2) , we get .
Therefore the required locus is , a straight line.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
What is the minimum area of a triangle with integral vertices ?
View SolutionThe distance between the points (acosα,asinα) and (acosβ,asinβ) is
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionIf P be a point on the parabola y^(2)=3(2x-3) and M is the foot of perpendicular drawn from the point P on the directrix of the parabola, then length of each sires of the parateral triangle SMP(where S is the focus of the parabola),is
View SolutionM is the foot of the perpendicular from a point P on a parabola y2=4ax to its directrix and SPM is an equilateral triangle, where S is the focus. Then find SP .
View SolutionIf Q is the foot of the perpendicular from a point p on the parabola y2=8(x−3) to its directrix. S is an equilateral triangle then find the lengh of side of the triangle.
View SolutionIf M is the foot of the perpendicular from a point P on a parabola to its directix and SPM is an equilateral triangle where S is the focus then SP=
View SolutionLet M be the foot of the perpendicular from a point P on the parabola y2=8(x−3) onto its directrix and let S be the foucs of the parabola. If △SPM is an equilateral triangle, then P is equal to
View SolutionIf Q is the foot of the perpendicular from a point P on the parabola y=8(x−3) to its directrix. S is the focus of the parabola and if SPQ is an equilateral triangle then the length of the side of the triangle is
View SolutionLet M be the foot of the perpendicular from a point P on the parabola y2=8(x−3) on to its directrix and let S be the focal of the parabola. If ΔSPM is an equalateral triangle, then P =
View SolutionM is the foot of the perpendicular from a point P on the parabola y2=8(x−3) to its directrix and S is an equilateral triangle, the length of side of the triangle is
View SolutionM is the foot of the perpendicular from a point P on a parabola y2=4ax to its directrix and SPM is an equilateral triangle, where S is the focus. Then find SP .
View SolutionIf P be a point on the parabola y2=3(2x−3) and M is the foot of perpendicular drawn from the point P on the directrix of the parabola, then find length of each sides of an equilateral triangle SMP(where S is the focus of the parabola).
View SolutionM is the foot of the perpendicular from a point P on a parabola y2=4ax to its directrix and SPM is an equilateral triangle, where S is the focus. Then find SP .
View SolutionIf Q is the foot of the perpendicular from a point p on the parabola y2=8(x−3) to its directrix. S is an equilateral triangle then find the lengh of side of the triangle.
View Solution
