m women and n men are too be seated in a row so that no two men sit together. If m>n then show that the number of wys in which they can be seated is m!(m+1)!(m−n+1)!
The correct Answer is:A
Since no two women should sit together and m>n. So, we first arrange m men in a row in m! ways. Now (m+1) places are there for n women to sit. This can be done in m+1Cn×n! ways.
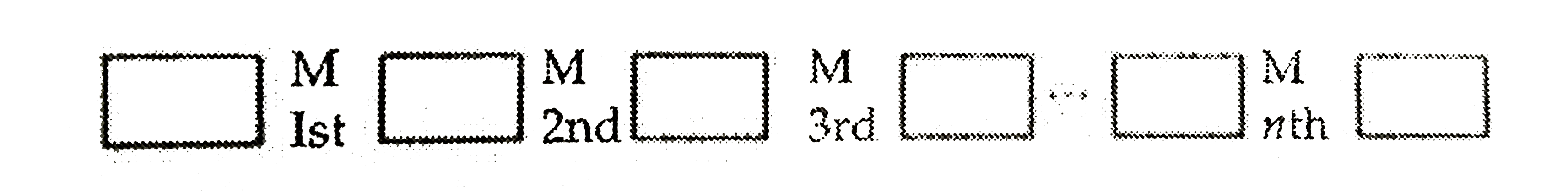
Hence, by the fundamental principle of counting the total number of seating arrangements is
m!×m+1Cn×n!=m!×(m+1)!(m+1−n)!n!×n!=m!(m+1)!(m−n+1)!
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs
111 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
m men and n women are to be seated in a row so that no two women sit together. If (m>n) then show that the number of ways in which they can be seated as m!(m+1)!(m−n+1)! .
View Solutionm men and w women are to be seated in a row so that no two women sit together.If m>w then the number of ways in which they can be seated is
View Solution
Knowledge Check
m men and w women are to be seated in a row so that no two women sit together. If m>w, then the number of ways in which they can be seated is :
Am!(m+1)!(m−w+1)!BmCm−w(m−w)!Cm+wCm(m−w)!Dnone of thesem men and w women are to be seated in a row so that all women sit together. The number of ways in which they can be seated is
A(m+1)!w!Bm!w!Cm!(w−1)!Dm+wCw5 men and 6 women have to be seated in a straight row so that no two women are together. Find the number of ways this can be done.
A48400B39600C9900D86400
If m red balls and n white balls are placed in a row so that no two white balls are together, prove that if m>n, the total number of ways in which this can be done is m+1Cn.
View SolutionAnswer these questions independently of each other
5 men and 4 women are to be seated for a dinner, In a row, such that no two men sit together. Find the number of ways in which this arrangements can be done.
View SolutionAnswer these questions independently of each other
5 men and 4 women are to be seated for a dinner, In a row, such that no two men sit together. Find the number of ways in which this arrangements can be done.
View SolutionAnswer these questions independently of each other
6 men and 3 women are to be seated for a dinner, In a row, such that no two women sit together. Find the number of ways in which this arrangements can be done.
View SolutionAnswer these questions independently of each other
5 men and 4 women are to be seated for a dinner, In a row, such that all the women do not sit together. Find the number of ways in which this arrangements can be done.
View Solution
