Match the following lists :

Video Solution
Text Solution
.
a. Since A is idempotent, we have
b. A is involuntary. Hence,
and
c. If A is nilpotent of index 2, then
d. A is orthogonal. Hence,
|
Topper's Solved these Questions
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Exercise (Numerical)
Explore 24 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:JEE Main Previous Year
Explore 11 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Exercise (Comprehension)
Explore 18 Videos
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:JEE Previous Year
Explore 10 Videos
- METHODS OF DIFFERENTIATIONBook:CENGAGEChapter:METHODS OF DIFFERENTIATIONExercise:Single Correct Answer Type
Explore 46 Videos
Similar Questions
Knowledge Check
Match the following list of microbes and their importance
 AABCD3412BABCD4321CABCD4213DABCD3142
AABCD3412BABCD4321CABCD4213DABCD3142Match the following list of microbes and their importance
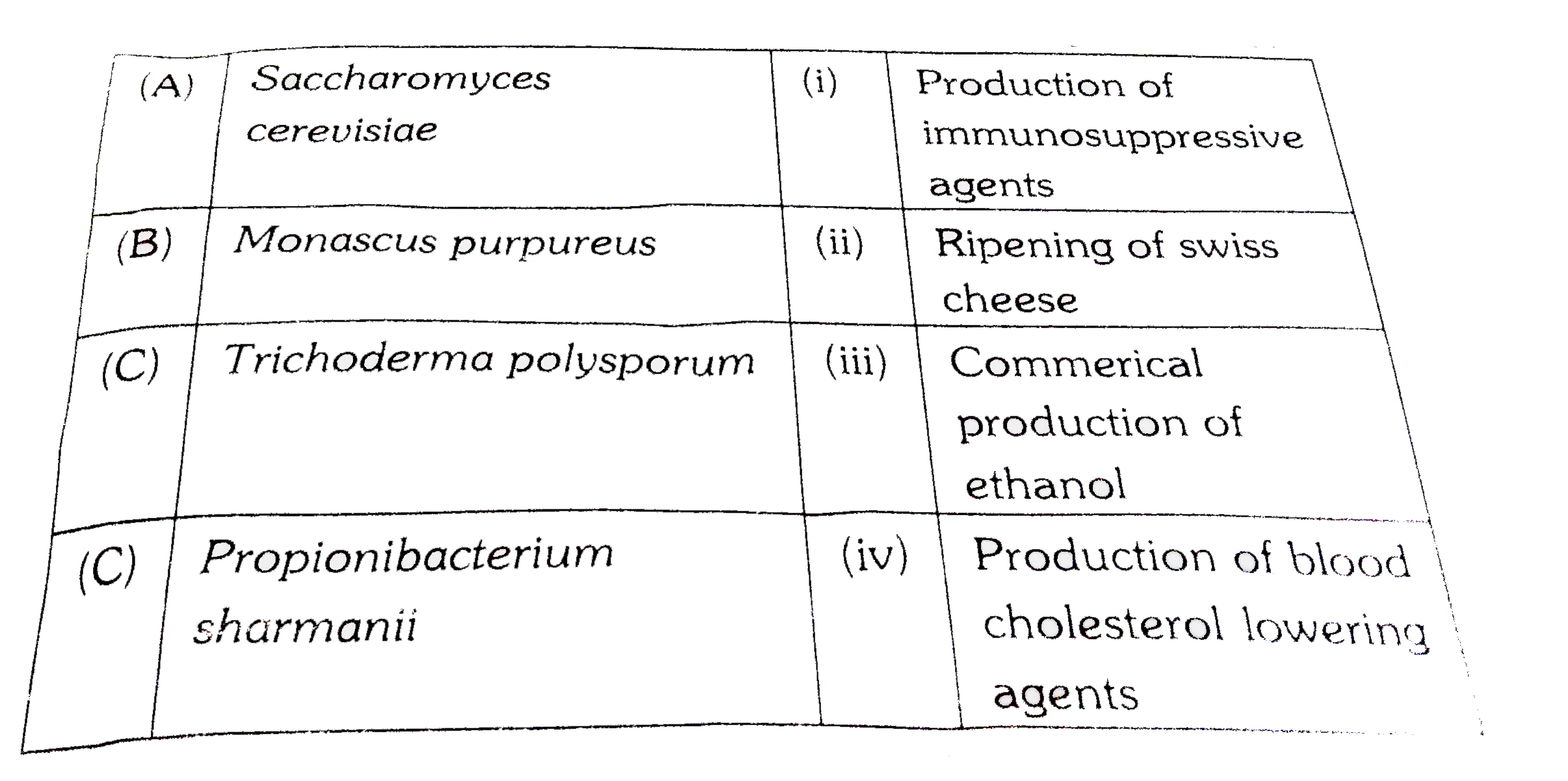 A(A)(B)(C)(D)(iii)(ii)(i)(iv)B(A)(B)(C)(D)(iv)(ii)(i)(iii)C(A)(B)(C)(D)(iii)(i)(iv)(ii)D(A)(B)(C)(D)(iii)(iv)(i)(ii)
A(A)(B)(C)(D)(iii)(ii)(i)(iv)B(A)(B)(C)(D)(iv)(ii)(i)(iii)C(A)(B)(C)(D)(iii)(i)(iv)(ii)D(A)(B)(C)(D)(iii)(iv)(i)(ii)Match the following list of microbes and their importan
 AA-iv B-iii C-ii D-iBA-iv B-ii C-i D-iiiCA-iii B-i C-iv D-iiDA-iii B-iv C-i D-ii
AA-iv B-iii C-ii D-iBA-iv B-ii C-i D-iiiCA-iii B-i C-iv D-iiDA-iii B-iv C-i D-ii
Match the following list of microbes and their importance :
View SolutionMatch the following list of bacteria and their commerically important products :

View SolutionMatch the following list of bacteria and their commerically important products :

View SolutionMatch the following list of bioactive substances and their roles :


View SolutionMatch the following list of bacteria and their commereially important products:

View Solution


