Match the following lists and then choose the correct code.

A
abcdprsq
B
abcdrsqp
C
abcdrqsp
D
abcdpqsr
Text Solution
The correct Answer is:B
a. f(x)=log3(5+4x−x2)
=log3(9−(x−2)2)
Now, −∞<9−(x−2)2≤9
But for f(x) to get defined, 0<9−(x−2)2≤9
or−∞<log3(9−(x−2)2)≤log39
or−∞<log3(9−(x−2)2)≤2
Hence, the range is (−∞,2].
b. f(x)=log3(x2−4x−5)
=log((x−2)2−9)
For f(x) to get defined, o<(x−2)2−9<∞
or limx→0logx<loge(x−2)2−9<limx→∞logx
or−∞<f(x)<∞
Hence, the range is R.
c. f(x)=log3(x2−4x+5)
=log3((x−2)2+1)
(x−2)2+1∈[1,∞)
or log3(x2−4x+5)∈[0,∞)
d. f(x)=log3(4x−5−x2)
=log3(−5−(x2−4x))
=log3(−1−(x−2)2)
Now, −1−(x−2)2<0 for all x.
Hence, the function is not defined.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqp - Question 2 - Select One
Match the following column and choose the correct code
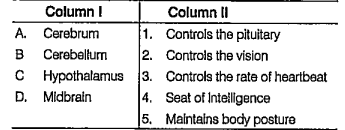 A
A B
B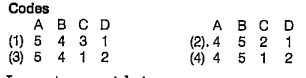 C
C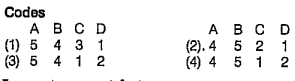 D
D
- Question 3 - Select One
Match the following two lists and choose the correct answer from the codes given below:
 AA-2,B-4,C-1,D-3BA-3,B-1,C-4,D-2CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
AA-2,B-4,C-1,D-3BA-3,B-1,C-4,D-2CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
Match the following columns and choose the correct code.
 View Solution
View SolutionMatch the following two lists and choose the correct answer from the codes given below:
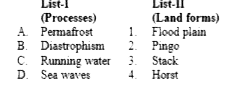 View Solution
View SolutionMatch the relation for derivatives given in List II with the relation given in List I and then choose the correct code.
 View Solution
View SolutionMatch List I with List II and choose the correct code
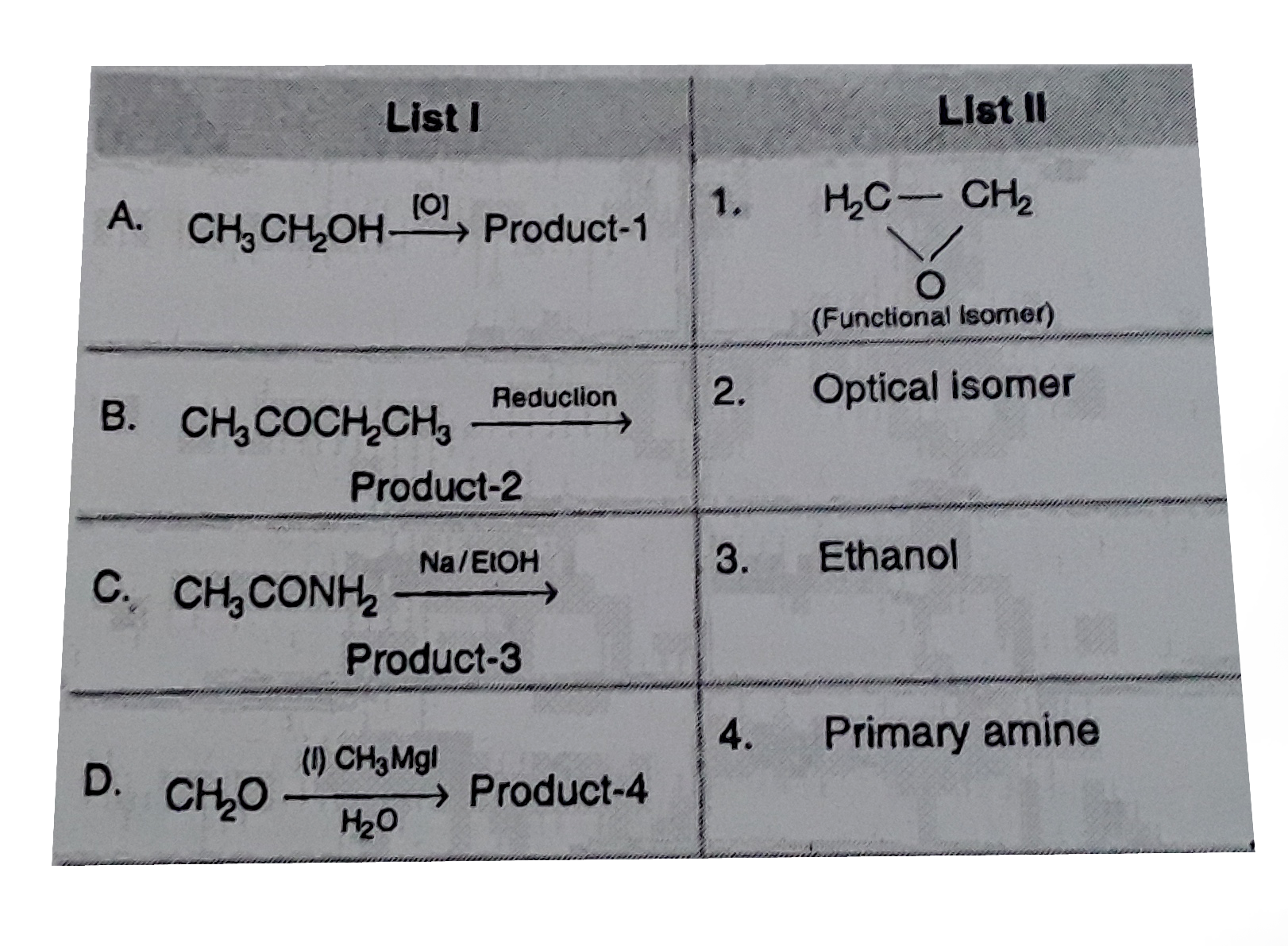 View Solution
View SolutionMatch the columns and choose the correct code.
 View Solution
View Solution



