Match the following lists and then choosen the corrct code.

A
abcdqpsr
B
abcdqrsq
C
abcdspqr
D
abcdqqsp
Text Solution
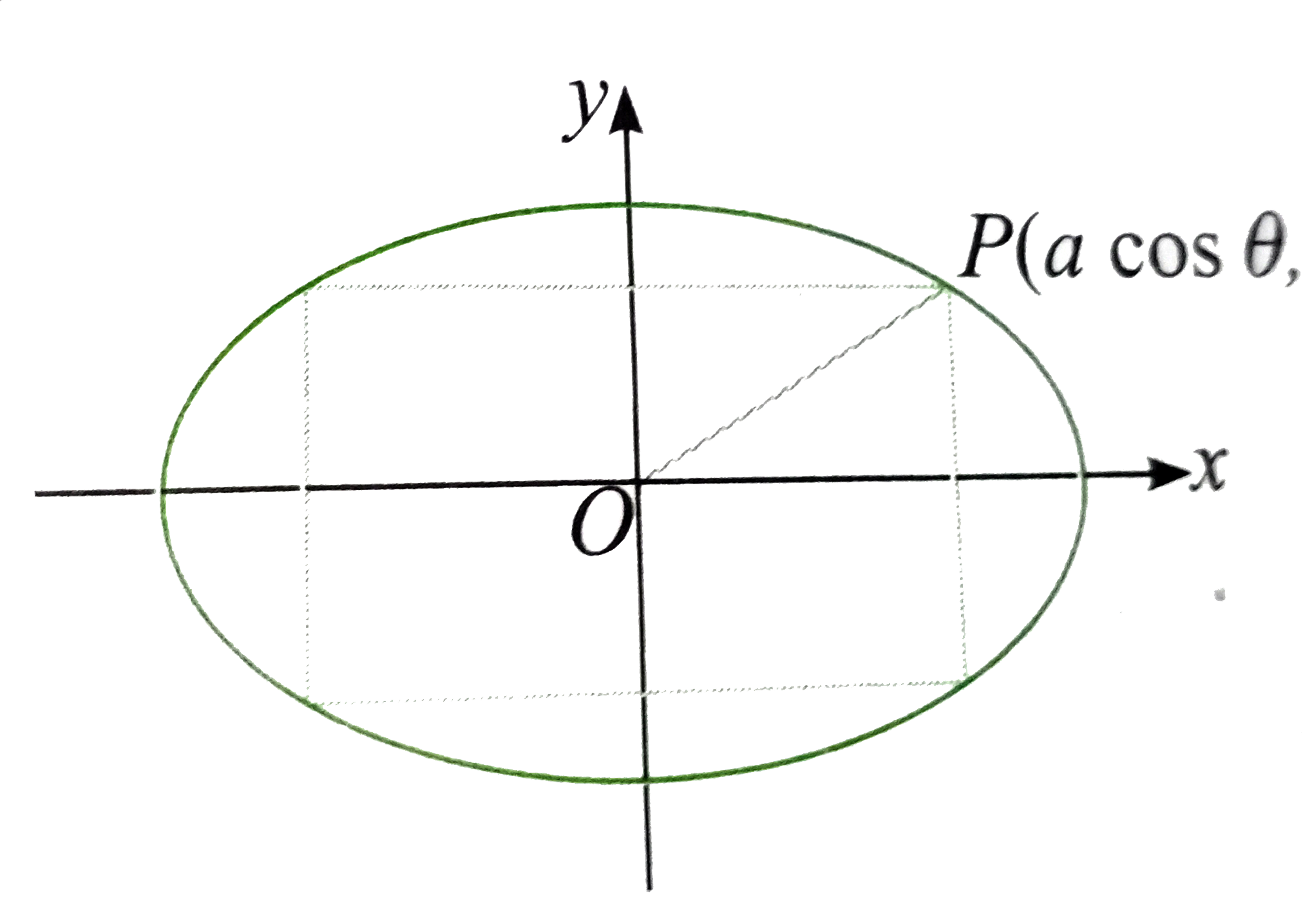
(a) Let one of the vertices of the rectangle be
P(acosθ,bsinθ). Then its area is
A=(2acosθ)(2bsinθ)=2absin2θ
Hence, Amax=2ab
Now, the area of recrtangle formed by the extermities of the latus rectum is
2ae×2b2a=4eb2
Given that
2ab=4eb2
or 2bae=1
or4b2a2e2=1
or 4(1−e2)e2=1
or(2e2−1)2=0
(b) 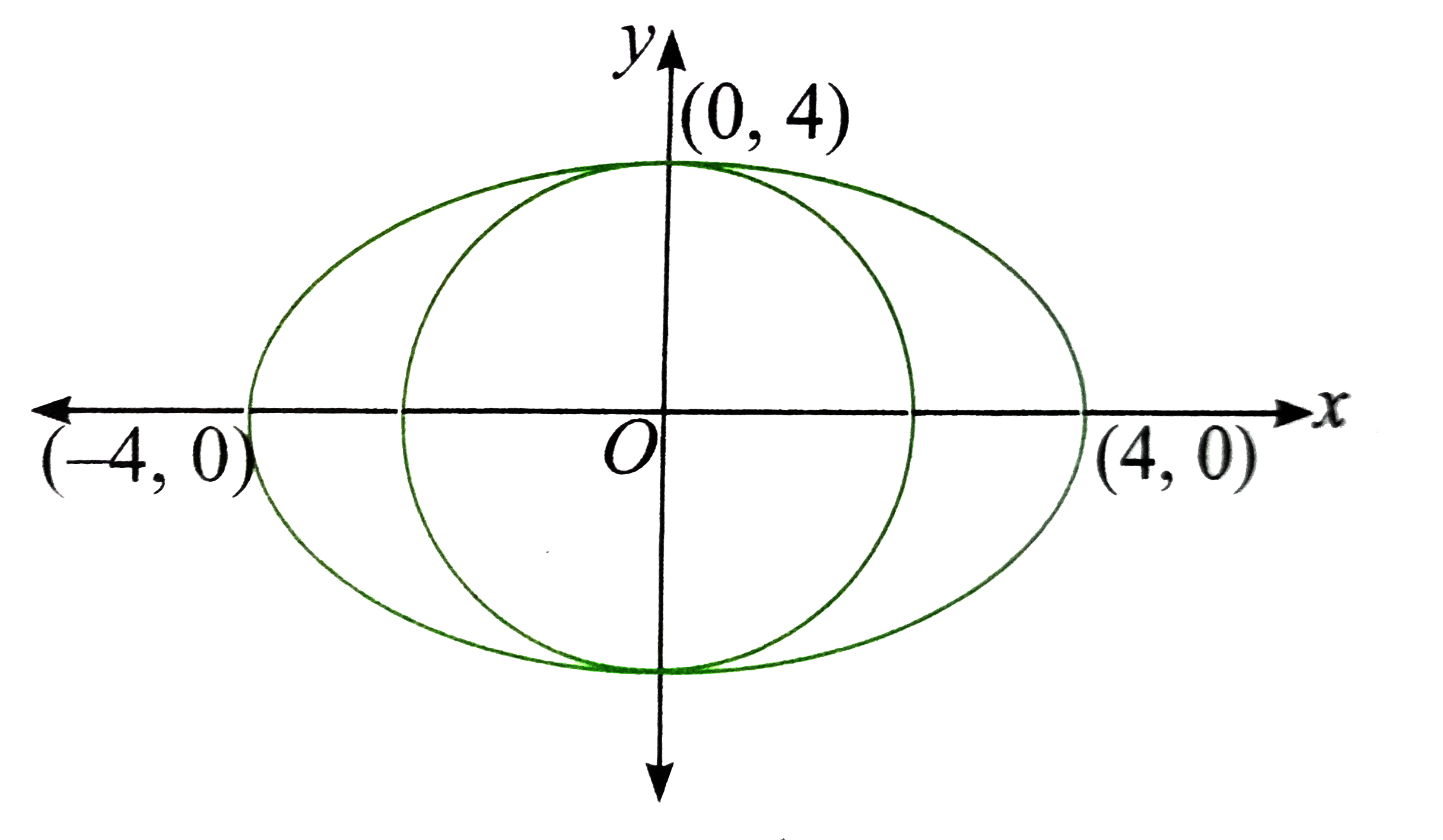
For the ellipse, the distacec between the foci, 2ae=8, and the length of the semi-minor axis is b=4 . Now,
b2=a2−a2e2
or 16=a2−16
ore2=32
or e=√1−1632=1√2
(c) Normal at point P(6,2) to the ellipse passes through its focus Q(5,2). Then P must be the extermity of the major axis, Now, ae=QR=1 (where R is ceter ) and a-ae=1

∴a=2
b2=a2−a2e2=4−1=3
or e=√1−34=12
(d) 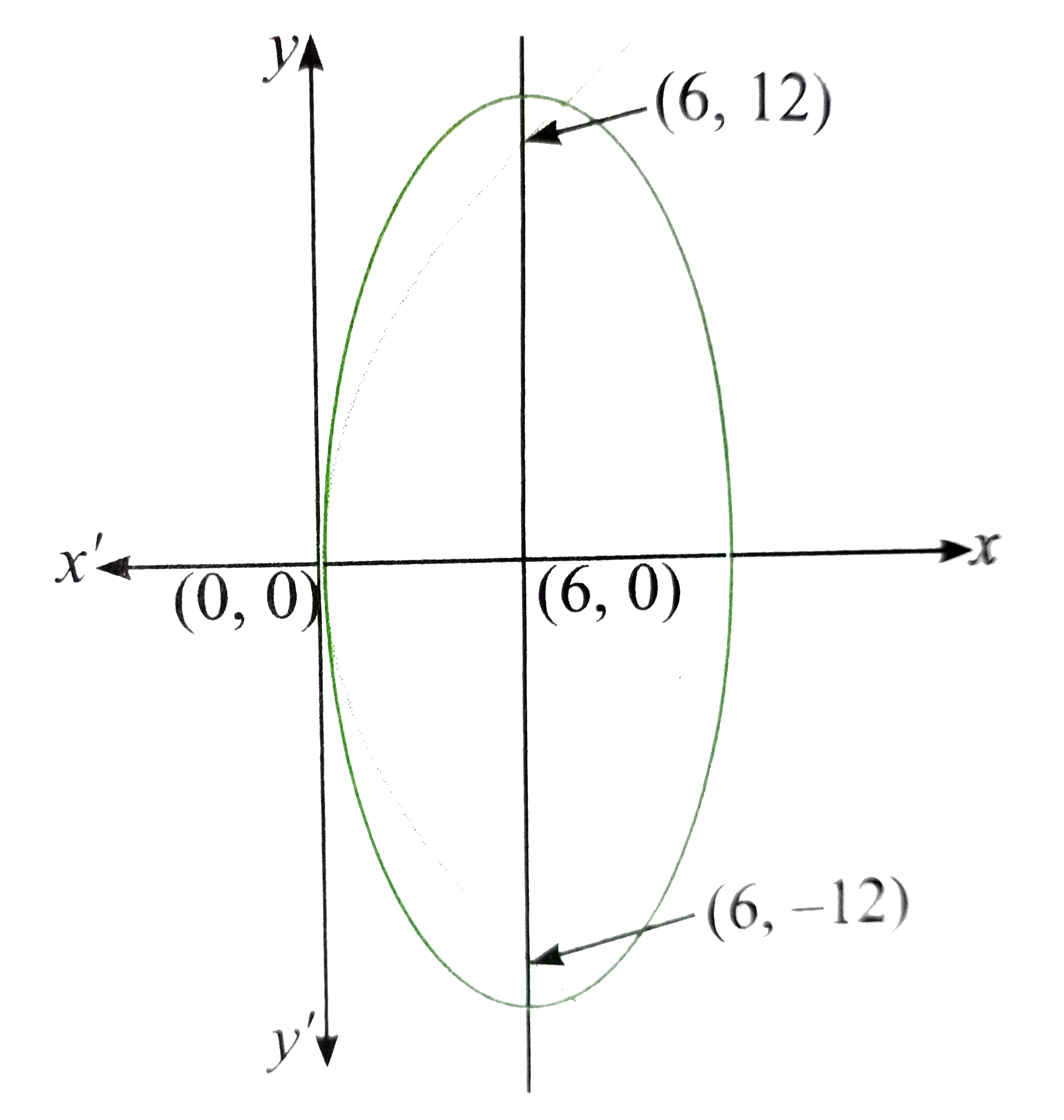
The extermities of the lotus rectum of teh parabola y2=24x are (6,±12). For ellipse 2be=24 and the extermity of the minro axis is (0,0). Hence a=6. Now,
a2=b2−b2e2
or b2=36+144=180
or e2√1−36180=√1−15=2√5
|
Similar Questions
Knowledge Check
Match the following lists and then choose the correct code.
 AabcdprsqBabcdrsqpCabcdrqspDabcdpqsr
AabcdprsqBabcdrsqpCabcdrqspDabcdpqsrMatch the following lists and then choose the correct code.
 AabcdqsrpBabcdpsrsCabcdqspsDabcdspqr
AabcdqsrpBabcdpsrsCabcdqspsDabcdspqrMatch the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
Match the following two lists and select the codes given below:

View SolutionMatch List I with List II and choose the correct code
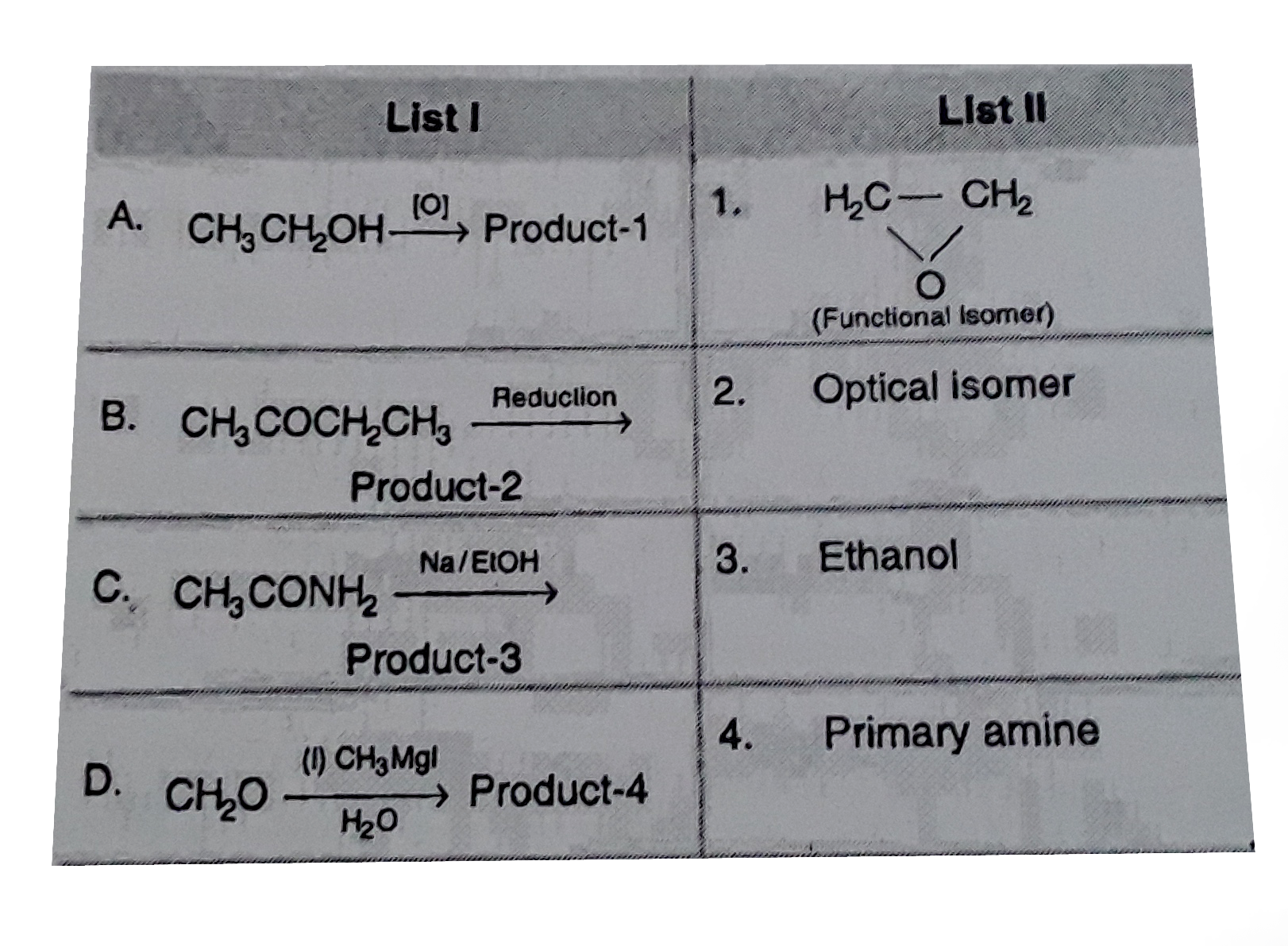
View SolutionMatch the List-I with List-II and choose the correct answer from the codes:
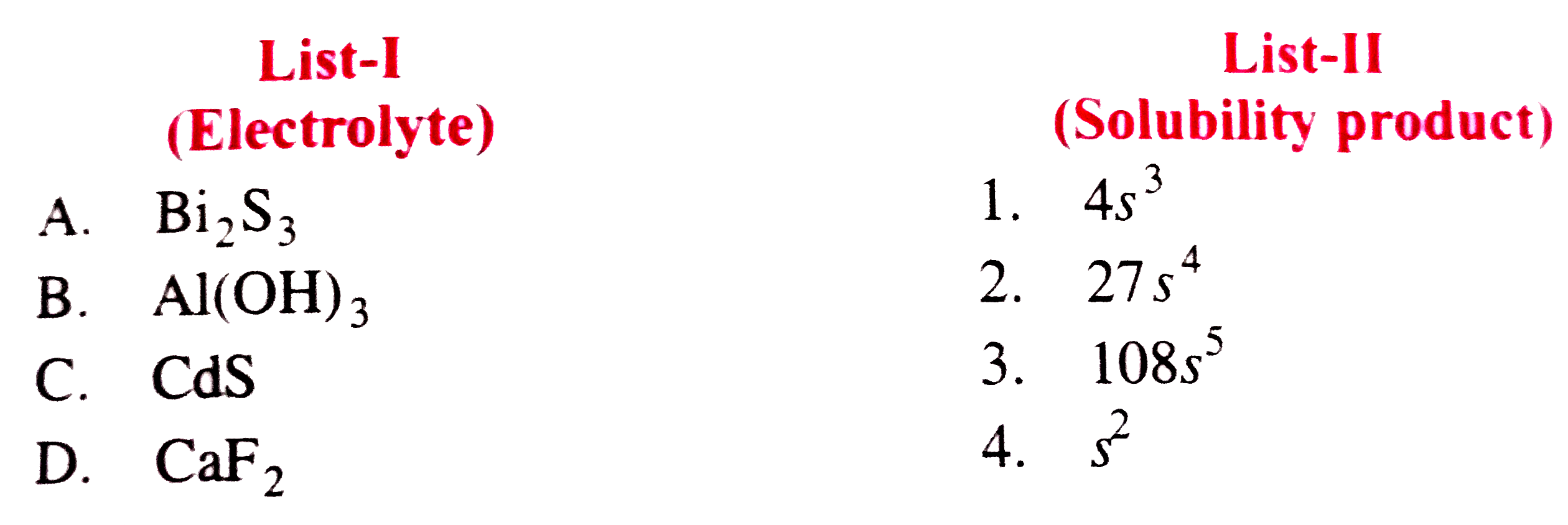
View SolutionMatch list I with list II and choose the correct answer from the codes

Code
View SolutionMatch list I with list II and then select the correct answer from the codes given below
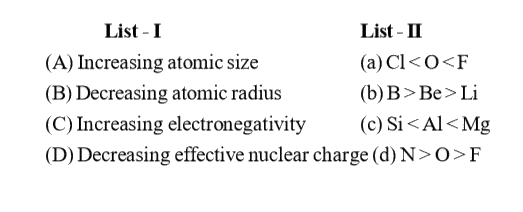
Codes :
View Solution
