Match the following lists and then choosen the corrct code.

A
abcdqpsr
B
abcdqrsq
C
abcdspqr
D
abcdqqsp
Text Solution
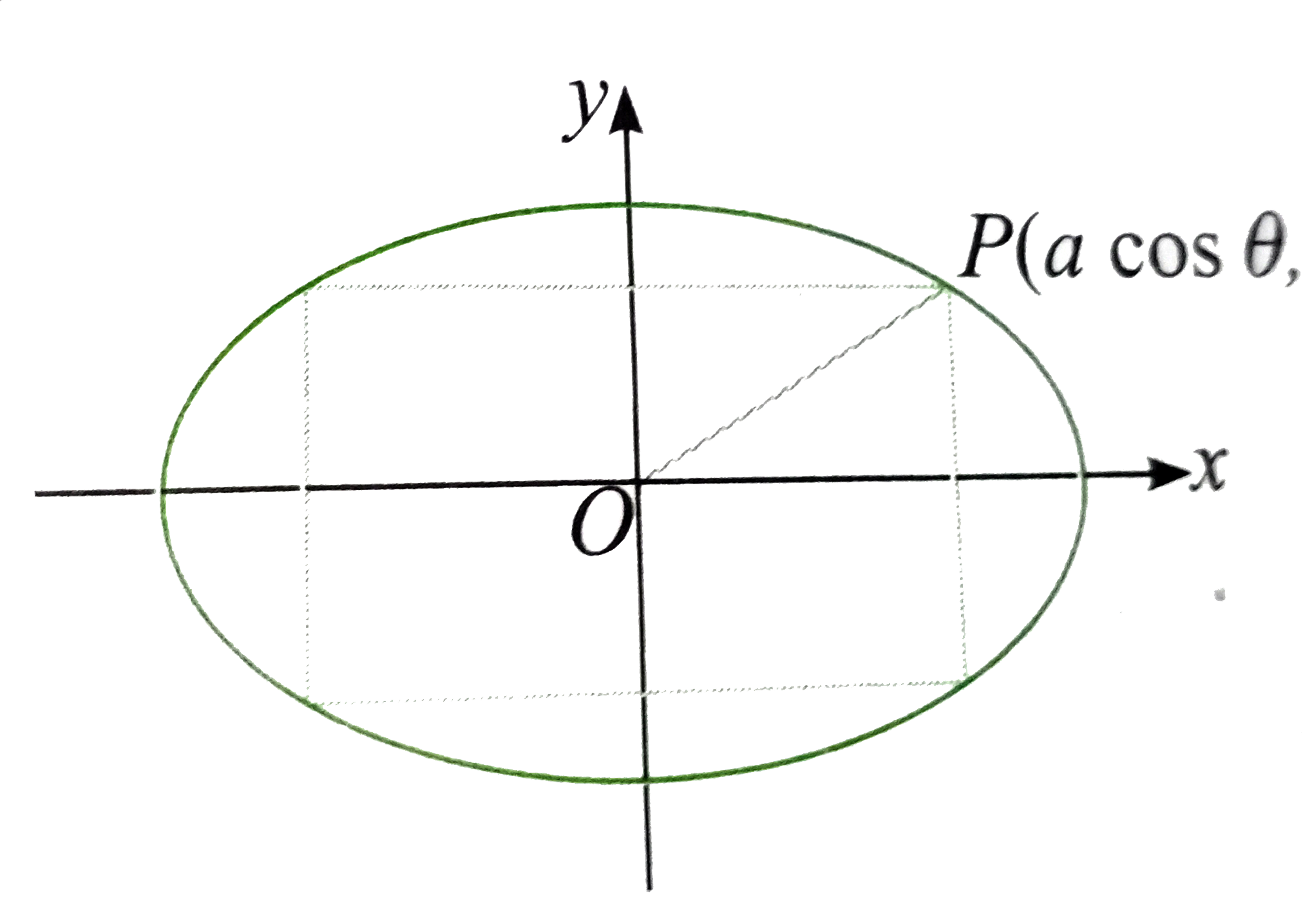
(a) Let one of the vertices of the rectangle be
P(acosθ,bsinθ). Then its area is
A=(2acosθ)(2bsinθ)=2absin2θ
Hence, Amax=2ab
Now, the area of recrtangle formed by the extermities of the latus rectum is
2ae×2b2a=4eb2
Given that
2ab=4eb2
or 2bae=1
or4b2a2e2=1
or 4(1−e2)e2=1
or(2e2−1)2=0
(b) 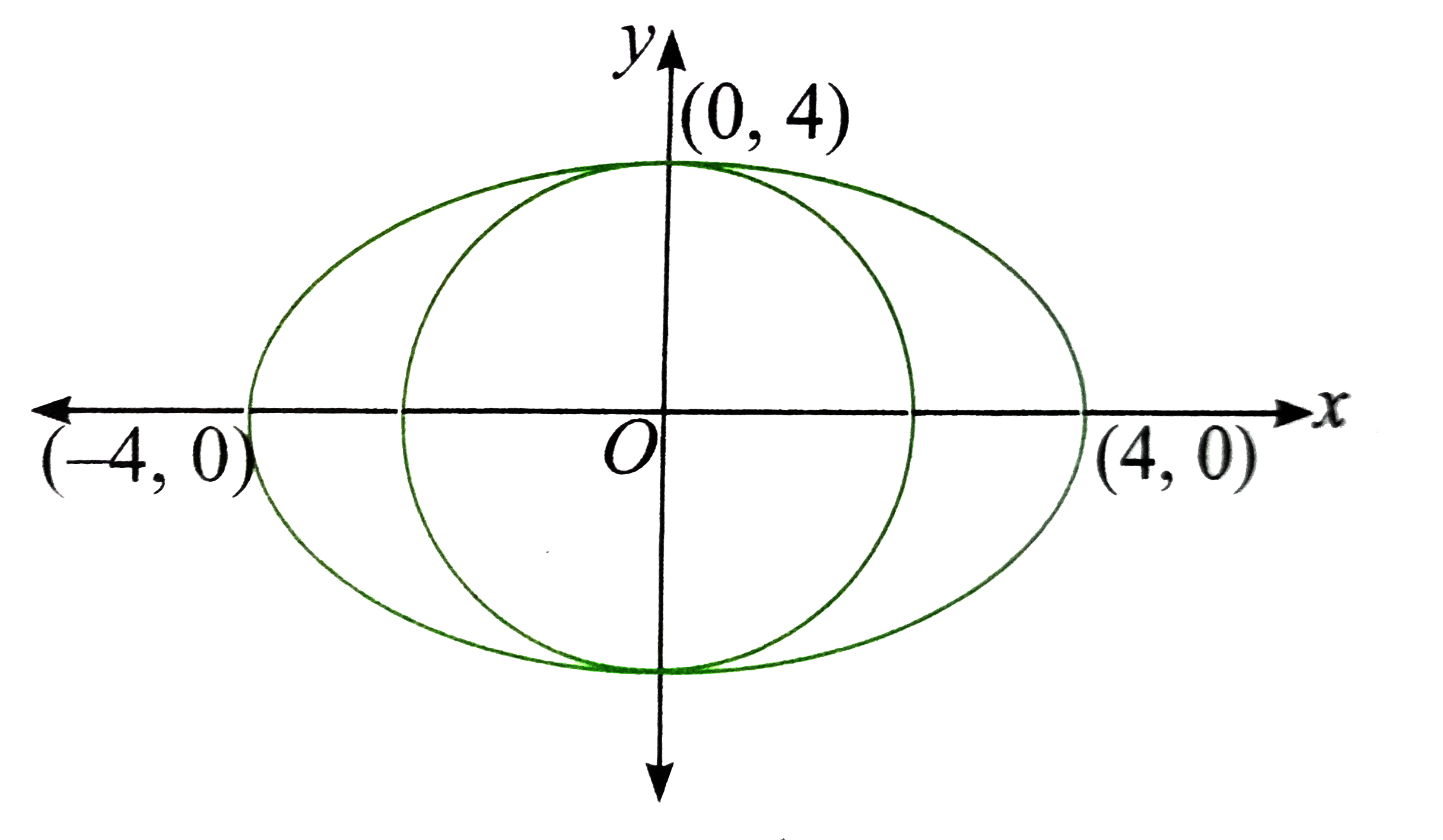
For the ellipse, the distacec between the foci, 2ae=8, and the length of the semi-minor axis is b=4 . Now,
b2=a2−a2e2
or 16=a2−16
ore2=32
or e=√1−1632=1√2
(c) Normal at point P(6,2) to the ellipse passes through its focus Q(5,2). Then P must be the extermity of the major axis, Now, ae=QR=1 (where R is ceter ) and a-ae=1

∴a=2
b2=a2−a2e2=4−1=3
or e=√1−34=12
(d) 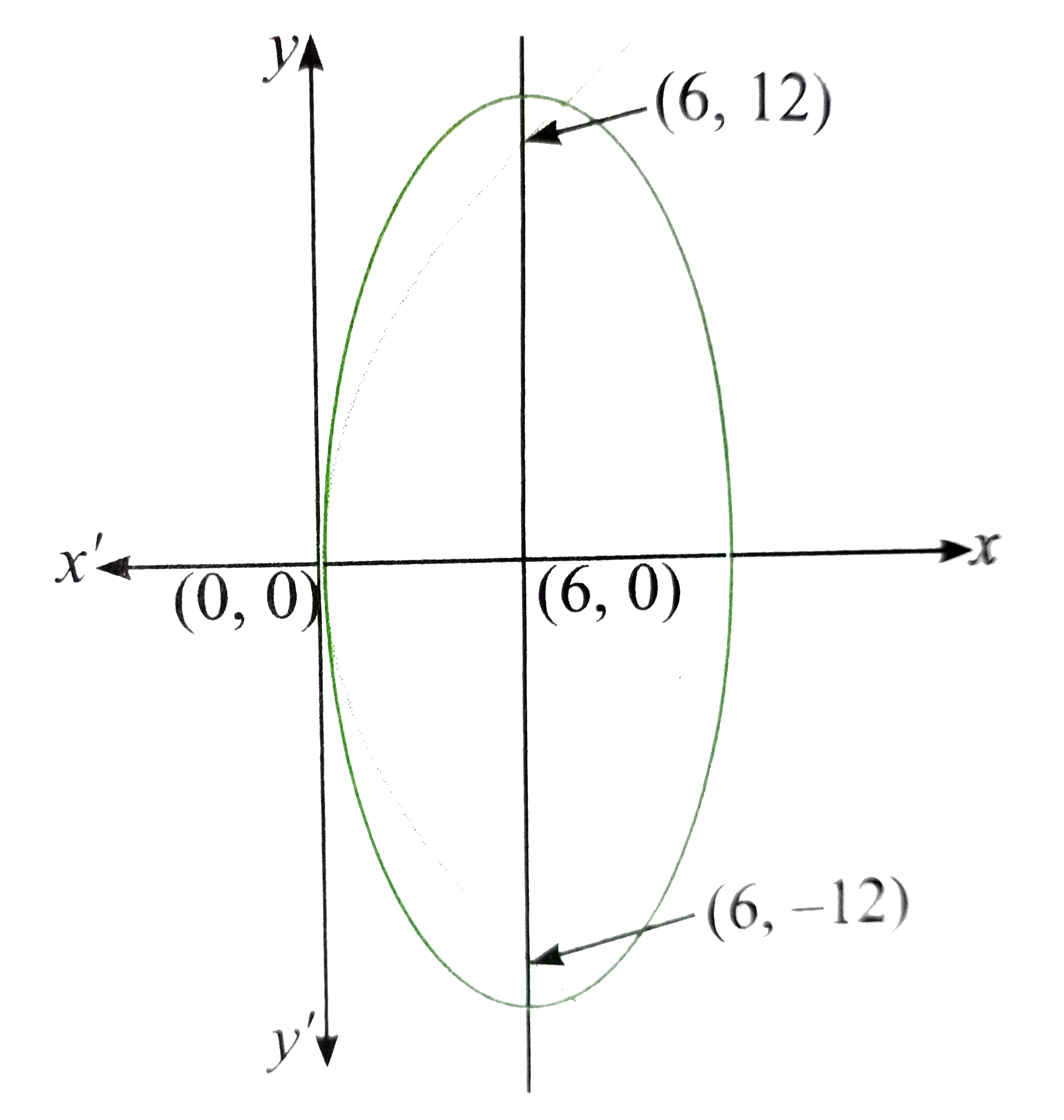
The extermities of the lotus rectum of teh parabola y2=24x are (6,±12). For ellipse 2be=24 and the extermity of the minro axis is (0,0). Hence a=6. Now,
a2=b2−b2e2
or b2=36+144=180
or e2√1−36180=√1−15=2√5
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the following lists and then choose the correct code.
 AabcdprsqBabcdrsqpCabcdrqspDabcdpqsr
AabcdprsqBabcdrsqpCabcdrqspDabcdpqsr - Question 2 - Select One
Match the following lists and then choose the correct code.
 AabcdqsrpBabcdpsrsCabcdqspsDabcdspqr
AabcdqsrpBabcdpsrsCabcdqspsDabcdspqr - Question 3 - Select One
Match the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
Match the following two lists and select the codes given below:
 View Solution
View SolutionMatch List I with List II and choose the correct code
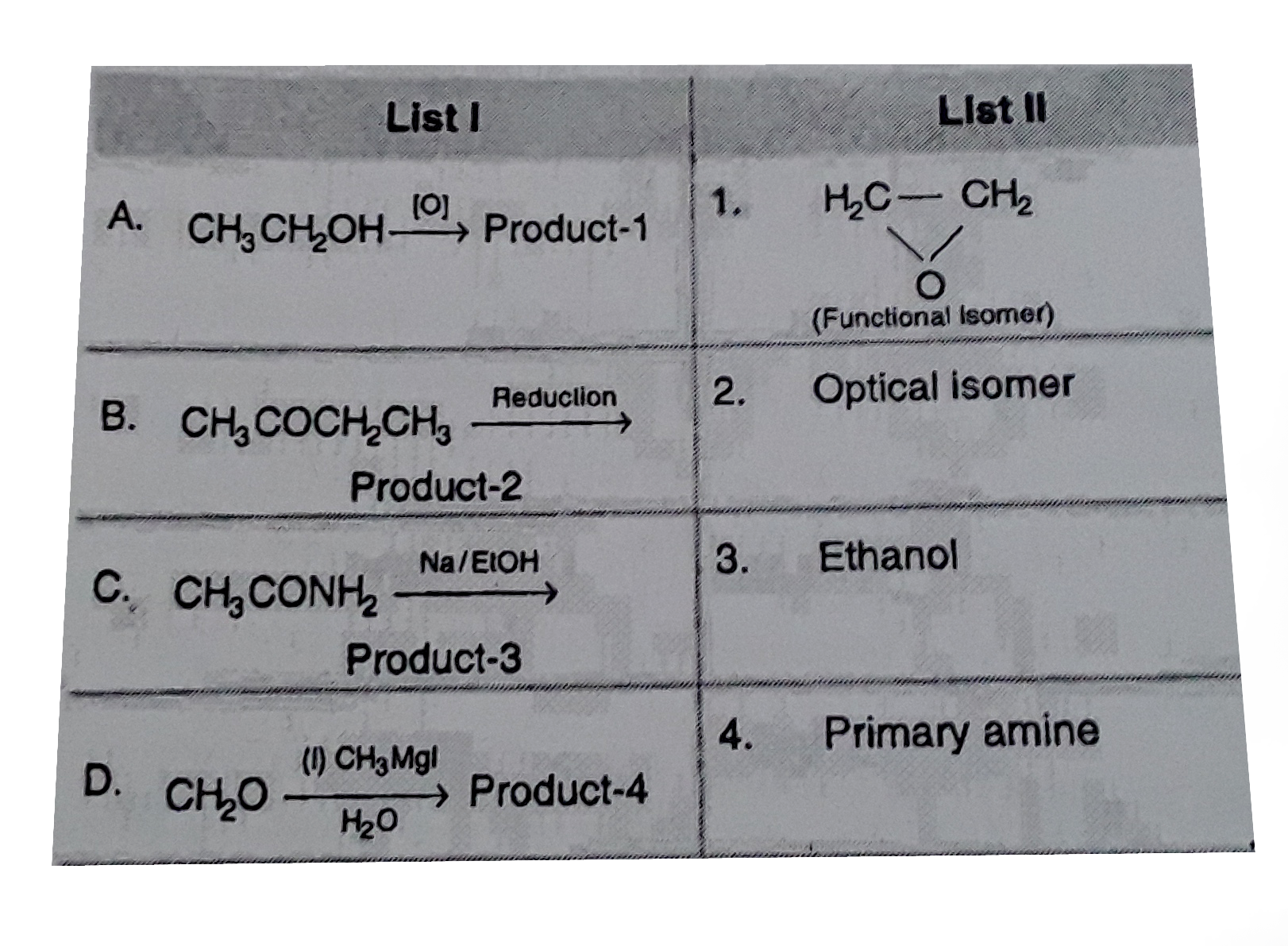 View Solution
View SolutionMatch the List-I with List-II and choose the correct answer from the codes:
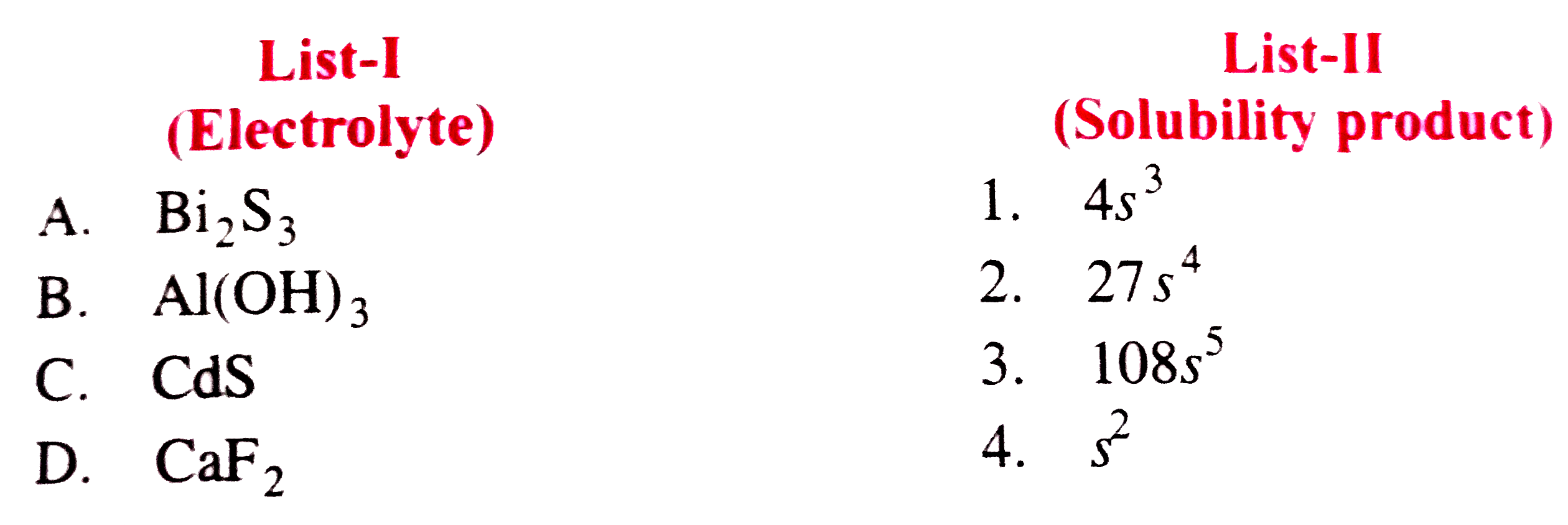 View Solution
View SolutionMatch list I with list II and choose the correct answer from the codes

CodeView SolutionMatch list I with list II and then select the correct answer from the codes given below
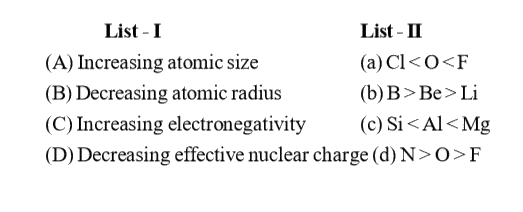
Codes :View Solution

