Minimize $Z = 4 x + 5 y$ subject to $2 x + y \geq 7, 2 x + 3 y \leq 15, x \leq 3, x \geq 0, y \geq 0$ solve using graphical method.

Video Solution

Text Solution

Verified by Experts

Corner point Method :
Step 1: Convert the inequations into the equations and draw the corresponding lines.
$2 x + y = 7 \Rightarrow \frac{x}{7 / 2} + \frac{y}{7} = 1$
$2 x + 3 y = 15 \Rightarrow \frac{x}{15 / 2} + \frac{y}{5} = 1$
$x = 3$
and $x \geq 0, y \geq 0,$ the solution lies in the first quadrant.
$∴$ ABCD is the feasible region.
Step 2: We find the coordinates of the vertices A, B, C
$A = (3, 1)$
$B (3, 3)$
$C (\frac{3}{2}, 4)$

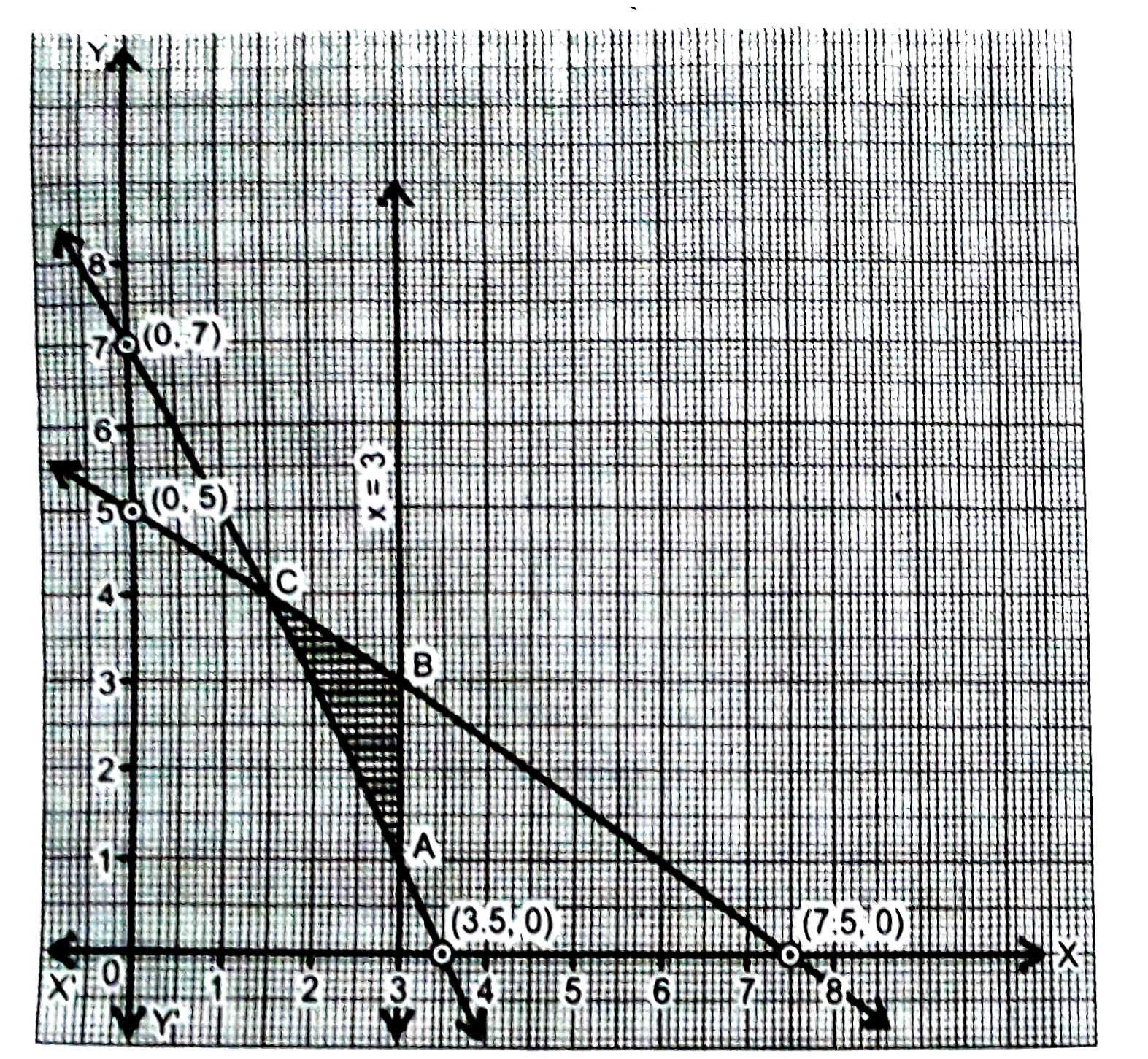
Step 3: We find the values of the objective function, $Z = 4 x + 5 y$ at the corner points (vertices) A, B and C respectively.
$Z (A) = 4 (3) + 5 (1) = 12 + 5 = 17$
$Z (B) = 4 (3) + 5 (3) = 12 + 15 = 27$
$Z (C) = 4 (\frac{3}{2}) + 5 (4) = 6 + 20 = 26 .$
$∴$ Z has minimum value 17 at (3,1).
$∴$ Optimum solution is $x = 3, y = 1$ with minimum value.

Updated on:21/07/2023

|

Class 12 MATHS MARCH 2016

Topper's Solved these Questions

Similar Questions

Knowledge Check

Minimum of $C = x + 3 y$
subject to $2 x + y \geq 6, x + y \geq 4, x \leq y, x \geq 0, y \geq 0$ is
A7
B8
C10
D6
Minimum of $Z = 5 x + 8 y$
subject to $x + y \geq 5, x \leq 4, y \leq 2, x \geq 0, y \geq 0$ is
A28
B13
C0
D52

GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS- MARCH 2016-SECTION II

Home
Ask Doubt
Profile