Minor defects are found on 7 to 10 new cars. If 3 of the 10 cars are selectred at random , what is the probability that 2 have minor defects ?
0.143
0.333
0.525
0.667
The correct Answer is:C
To solve the problem of finding the probability that 2 out of 3 randomly selected cars have minor defects when there are 7 defective cars out of a total of 10, we can follow these steps:
Step 1: Identify the total number of defective and non-defective cars
- Total cars = 10
- Defective cars = 7
- Non-defective cars = 10 - 7 = 3
Step 2: Determine the number of ways to choose 2 defective cars
To find the number of ways to choose 2 defective cars from the 7 defective cars, we use the combination formula nCr, which is given by:
nCr=n!r!(n−r)!
For our case, we need to calculate 7C2:
7C2=7!2!(7−2)!=7×62×1=21
Step 3: Determine the number of ways to choose 1 non-defective car
Next, we find the number of ways to choose 1 non-defective car from the 3 non-defective cars:
3C1=3!1!(3−1)!=31=3
Step 4: Calculate the total number of favorable outcomes
The total number of favorable outcomes (choosing 2 defective and 1 non-defective) is the product of the combinations calculated in Steps 2 and 3:
Favorable outcomes=7C2×3C1=21×3=63
Step 5: Determine the total number of ways to choose any 3 cars from 10
Now, we calculate the total number of ways to choose any 3 cars from the 10 cars:
10C3=10!3!(10−3)!=10×9×83×2×1=120
Step 6: Calculate the probability
Finally, we can find the probability that 2 out of the 3 selected cars have minor defects by dividing the number of favorable outcomes by the total number of outcomes:
P(2 defective)=Favorable outcomesTotal outcomes=63120
Simplifying this fraction gives:
P(2 defective)=2140≈0.525
Conclusion
Thus, the probability that 2 out of the 3 selected cars have minor defects is approximately 0.525.
---
- Total cars = 10
- Defective cars = 7
- Non-defective cars = 10 - 7 = 3
To find the number of ways to choose 2 defective cars from the 7 defective cars, we use the combination formula nCr, which is given by:
Next, we find the number of ways to choose 1 non-defective car from the 3 non-defective cars:
The total number of favorable outcomes (choosing 2 defective and 1 non-defective) is the product of the combinations calculated in Steps 2 and 3:
Now, we calculate the total number of ways to choose any 3 cars from the 10 cars:
Finally, we can find the probability that 2 out of the 3 selected cars have minor defects by dividing the number of favorable outcomes by the total number of outcomes:
Thus, the probability that 2 out of the 3 selected cars have minor defects is approximately 0.525.
Topper's Solved these Questions
Similar Questions
Bulbs are packed in cartons each containing 40 bulbs, seven hundred cartons were examined for defective bulbs and the results are given in the following table.
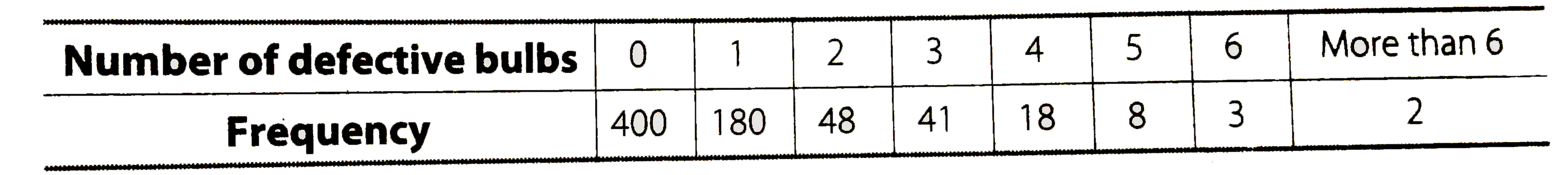
One carton was selected at random. What is the probability that it has
i) no defective bulb?
ii) defective bulbs from 2-6?
iii) defective bulbs less than 4?
View SolutionThere are 10 defective bulbs in a group of 100 bulbs. If a sample of 8 bulbs are selected at random then find the probability that:
(i) in this sample 3 bulbs are defective and 5 are non-defective.
(ii) in this sample at least one bulb is defective.
View Solution
Knowledge Check
Rent-a-Rek has 27 cars available for rental. Twenty of these are compact, and 7 are midsize. If two cars are selected at random, what is the probability that both are compact?
A0.576B0.0598C0.481D0.541In a batch of 10 light bulbs , 2 are defective . If 3 of the bulbs are chosen at random, what is the probability that at least 1 of the chosen bulbs is defective ?
A815B715C310D14
A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?
View SolutionA carton of 24 bulbs contain 6 defactive bulbs. One but is drawn at random. What is the probability that the bulbs is not defactive? If the bulb selected is defective and it is not replaced and a second bulb is selected at random from the rest, what is the probability that the second bulb is defactive?
View SolutionA lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, then what is the probability that there will be atleast one defective watch ?
View Solution(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective ?
View SolutionA basket contains 20 apples and 10 oranges out of which 5 apple and 3 orange are defective. If a person takes out 2 at random. What is the probability that either both are apples or both are good?
View SolutionFrom a well shuffled deck of 52 cards, 4 cards are drawn at random. What is the probability that all the drawn cars are of the same colour.
View Solution
