Normal to the circle $x^{2} + y^{2} = 4$ divides the circle having centre at (2,4) and radius 2 in the ares of ratio $(π - 2) : (3 π + 2)$ . Then the normal can be

Text Solution

Verified by Experts

The correct Answer is:1,4

Normal to the circles $x^{2} + y^{2} = 4$ passes through its centre (0,0)

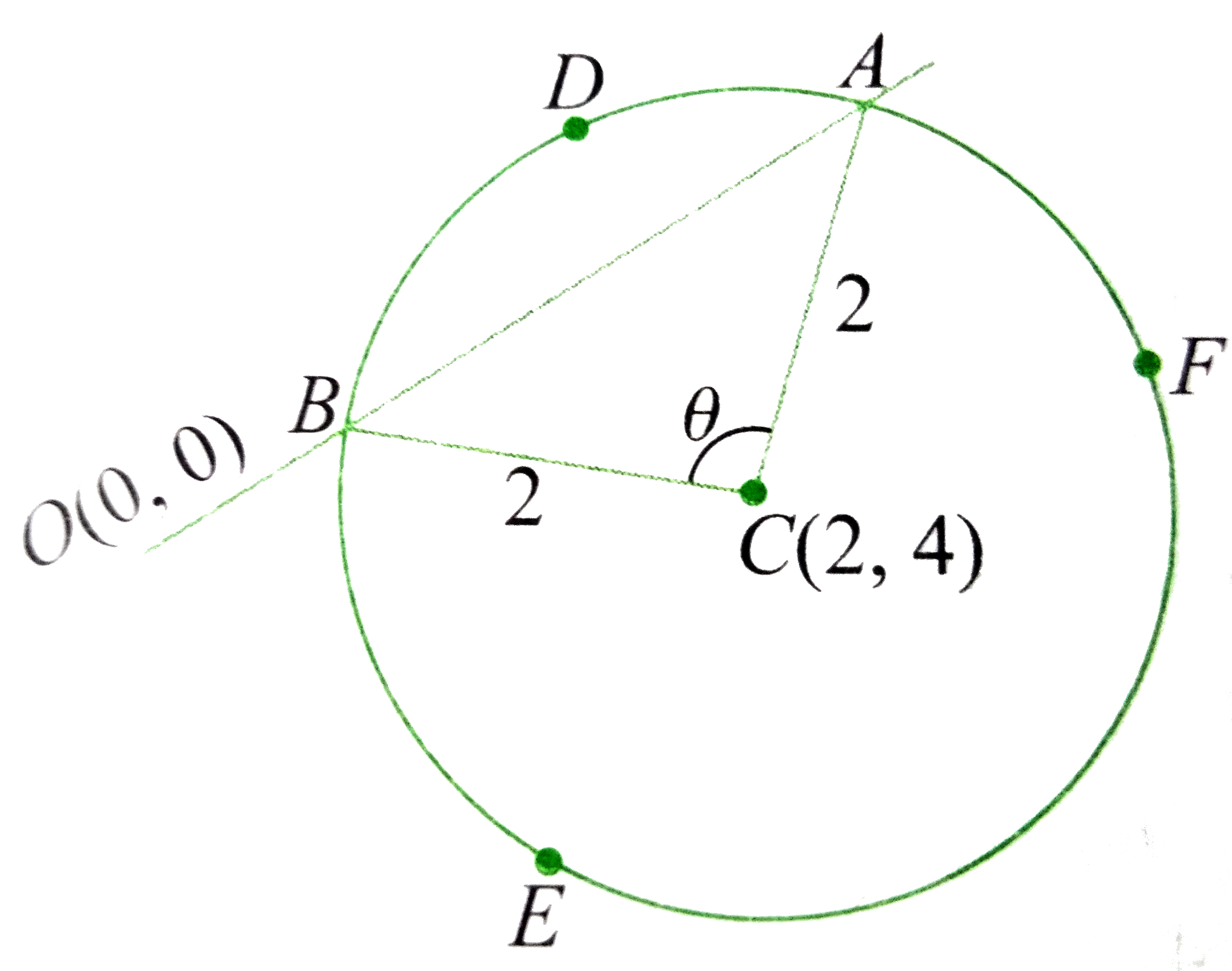
So, equation of normal is $y = m x$ .
Now, according to the question.
$\frac{Area of regio ADBA}{Area of regioN abefa} = \frac{π - 2}{23 π + 2}$
$∴ \frac{[\frac{π {(2)}^{2}}{2 π} . θ - \frac{1}{2} {(2)}^{2} sin θ]}{π {(2)}^{2} - [\frac{π {(2)}^{2}}{2 π} . θ - \frac{1}{2} {(2)}^{2} sin θ]} = \frac{π - 2}{3 π + 2}$
$\Rightarrow θ = \frac{π}{2}$
$∴$ Distance of centre of circle from line $= 2 cos . \frac{π}{4}$
$\Rightarrow \frac{| 4 - 2 m |}{\sqrt{1 + m^{2}}} = \sqrt{2}$
$\Rightarrow m = 1, 7$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The line 4x+3y-4=0 divides the circumference of the circle centred at (5,3) in the ratio 1:2. Then the equation of the circle is
A $x^{2} + y^{2} - 10 x - 6 y - 66 = 0$
B $x^{2} + y^{2} - 10 x - 6 y + 100 = 0$
C $x^{2} + y^{2} - 10 x - 6 y + 66 = 0$
Dnone of these
Question 2 - Select One
Radius of the circle centred at $(3, - 2)$ , or maximum area contained in the circle $x^{2} + y^{2} - 4 x + y = 0$ is
A $(1 / 2) (\sqrt{17} - \sqrt{13})$
B $1 / \sqrt{2}$
C $\sqrt{2}$
Dnone of these
Question 3 - Select One
The centre and radius of the circle ${(x + 2)}^{2} + {(y + 4)}^{2} = 9$ are
A(2, 4) and 3
B $(- 2, - 4) and 3$
C $(- 2, - 4)$ and 9
D $(2, - 4)$ and 3

CENGAGE PUBLICATION-CIRCLE -Multiple Correct Anser Type

Home
Ask Doubt
Profile