Number of binary operations on the set {a, b} are (A) 10 (B) 16 (C) 20 (D) 8
10
16
20
8
The correct Answer is:B
Step by step video, text & image solution for Number of binary operations on the set {a, b} are (A) 10 (B) 16 (C) 20 (D) 8 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Objective Type Questions (B. Fill in the Blanks)
5 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Objective Type Questions (C. True/False Questions)
5 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1 (e) (Long Answer Type Questions (I))
8 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MOCK TEST SECTION D
6 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - CHAPTER TEST 11
11 Videos
Similar Questions
Knowledge Check
Let '∗' be the binary operation defined on the set Z of all integers as a∗b=a+b+1 for all a, b ∈Z. The identity element w.r.t. this operations is
A−1B−2C1D0
The number of binary operations that can be defined on a set of 2 elements is
View SolutionHow many cubes are there in the group?
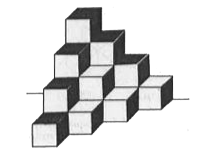 (A)20
(B)10
(C)16
(D)8
(A)20
(B)10
(C)16
(D)8
View SolutionConsider the binary operation ∗ on the set {1,2,3,4,5} defined by a∗b=min.{a,b}. Write the operation table of the operation ∗.
View SolutionLet A=NxN, and let * be a binary operation on A defined by (a,b)⋅(c,d)=(ad+bc,bd) for all (a,b),c,d)∈NxN. Show that : '⋅' is commutative on A '⋅′ is associative onA A has no identity element.
View SolutionLet A=N×N , and let * be a binary operation on A defined by (a, b)⋅(c, d)=(ad+bc, bd) for all (a, b), (c, d)∈N×N. Show that: * is commutative on A. (ii) * is associative on A.
View SolutionThe number of commutative binary operations that can be defined on a set of 2 elements is
View SolutionOn the set Q+ of all positive rational numbers a binary operation * is defined by a∗b=ab2 for all a, b∈Q+ . The inverse of 8 is
View Solution
