Number of ordered pair (a,b) the set A={1,2,3,4,5} so that the functon f(x)=x33+a2x2+bx+10 is an injective mapping ∀x∈R:
13
14
15
16
The correct Answer is:C
Step by step video solution for Number of ordered pair (a,b) the set A = {1,2,3,4,5} so that the functon f(x)=(x^(3))/(3)+a/2 x ^(2)+ bx+10 is an injective mapping AA x in R: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VK JAISWAL ENGLISHCHAPTER - FUNCTION EXERCISE - ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT23videos
FUNCTION
- BOOK - VK JAISWAL ENGLISHCHAPTER - FUNCTION EXERCISE - COMPREHENSION TYPE PROBLEMS15videos
FUNCTION
- BOOK - VK JAISWAL ENGLISHCHAPTER - ELLIPSE EXERCISE - Exercise-4 : Subjective Type Problems2videos
ELLIPSE
- BOOK - VK JAISWAL ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise-4 : Subjective Type Problems3videos
HYPERBOLA
Similar Questions
Knowledge Check
- Question 1 - Select One
The solution set of 2x+13<3x−25x∈R on the number line is
A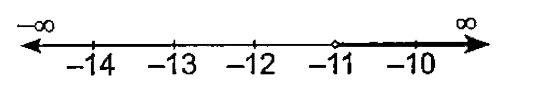 B
B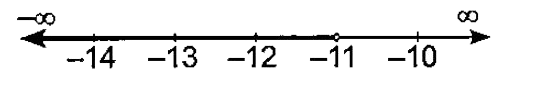 C
C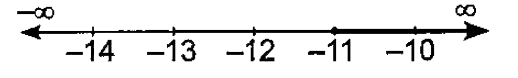 D
D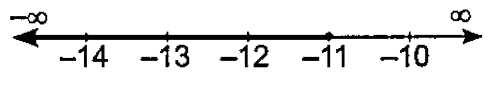
The number of ordered pairs (a,b) where a,b are integers satisfying the inequality min (x2+(a−b)x+(1−a−b))>max(−x2+(a+b)x−(1+a+b)∀x∈R, is :
View SolutionA function f :R→R is defined by f(x)=2x3+3 . Show that f is a bijective mapping .
View SolutionShow that f:R→R defined by f(x)=(x−1)(x−2)(x−3) is surjective but not injective.
View SolutionThe value of x,∀x∈R which satisfy the equation (x−1)∣∣x2−4x+3∣∣+2x2+3x−5=0 is
View SolutionThe number of integral values of a for which f(x)=x3+(a+2)x2+3ax+5 is monotonic in ∀x∈R
View SolutionIf f:R→R be the function defined by f(x)=sin(3x+2)∀x∈R. Then, f is invertible.
View SolutionThe function f:R→R defined as f(x)=3x2+3x−43+3x−4x2 is :
View Solution

