Number of solutions 2sin(|x|)=4|cosx|∈[−π,π] is equal to
A
2
B
4
C
6
D
None of these
Video Solution
Text Solution
The correct Answer is:B
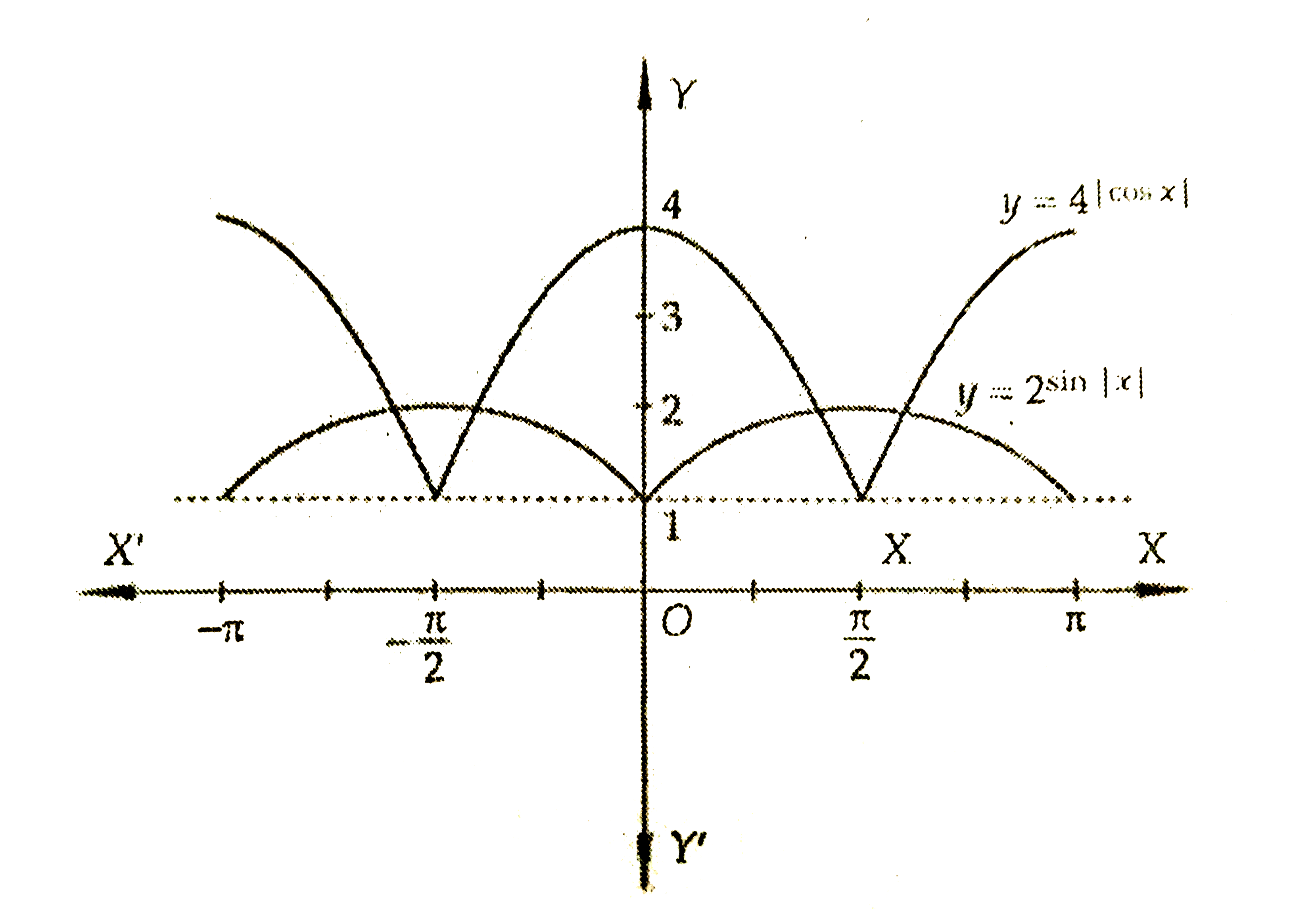
The total number of solutions of the given equation is equal to the number of points of intersection of curves y=4|cosx| and y=2sin|x|. Clearly, these two curves intersect a four points. So, there are four solutions of the given equation in the interval [−π,π].
|
Topper's Solved these Questions
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise
30 Videos
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test
30 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
Similar Questions
Knowledge Check
Total number of solution of 2cosx=|sinx|in[−2π,5π] is equal to :
A12B14C16D15Total number of solutions of sin4x+cos4x=sinx⋅cosx in [0,2π] is equal to
A2B4C6D8Find the total number of solution of sin4x+cos4x=sinxcosx in [0,2π] is equal to
A2B4C6D8
The total number of solutions of loge|sinx|=−x2+2x∈[0,π] is equal to
View SolutionNumber of solution 2cosx=|sinx| in [0,2π] is
View SolutionThe number of solutions of sin7x+cos7x=1,x∈[0,4π] is equal to
View SolutionThe total number of solutions of cosx=√1−sin2x in [0,2π] is equal to
View SolutionNumber of solution of sinxcosx−3cosx+4sinx−13>0 in [0,2π] is equal to
View Solution
