O is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC.
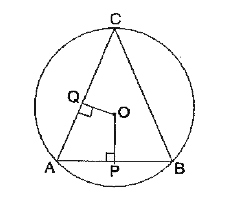
O is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC.

A

3 cm, 4 cm

B

4 cm, 3 cm

C

2 cm, 3 cm

D

3.5 cm, 2.5 cm

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

|
Answer

Step by step video, text & image solution for O is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.

Updated on:21/07/2023
Class 7MATHSPERIMETER AND AREA

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :

    A√3172cm
    B√1192cm
    C√1152cm
    D√3132cm

  • O is the centre of the circle of radius 6 cm and P is the mid -point of a chord AB .The length OP is 3 cm. The area (in sq cm ) of △AOB is :

    A26π
    B24π
    C20π
    D18π

  • O is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is

    A3.015 cm.
    B3.205 cm.
    C3.025 cm.
    D3.125 cm.