OP……...OR, where O is the centre of the circle, P lies on the circle and R lies in the exterior of the circle.
To solve the question OP - OR, where O is the center of the circle, P lies on the circle, and R lies in the exterior of the circle, we can follow these steps:
1. Understanding the Circle:
- We have a circle with center O.
- Point P is located on the circumference of the circle, which means the distance from O to P is the radius of the circle, denoted as OP.
2. Identifying Point R:
- Point R is located outside the circle. This means that the distance from O to R (denoted as OR) is greater than the radius of the circle.
3. Comparing Distances:
- Since P is on the circle, the distance OP is equal to the radius (let's denote it as r).
- The distance OR, being outside the circle, must be greater than the radius. Therefore, we can say that OR > r.
4. Establishing the Relationship:
- From the above points, we can conclude that OP < OR. This means that the distance from the center O to point P (on the circle) is less than the distance from the center O to point R (outside the circle).
5. Final Conclusion:
- Thus, we can summarize that OP < OR, indicating that the distance to point R (which is outside the circle) is greater than the distance to point P (which is on the circle).
Final Statement:
Therefore, we conclude that OP is less than OR: OP < OR.
---
- We have a circle with center O.
- Point P is located on the circumference of the circle, which means the distance from O to P is the radius of the circle, denoted as OP.
- Point R is located outside the circle. This means that the distance from O to R (denoted as OR) is greater than the radius of the circle.
- Since P is on the circle, the distance OP is equal to the radius (let's denote it as r).
- The distance OR, being outside the circle, must be greater than the radius. Therefore, we can say that OR > r.
- From the above points, we can conclude that OP < OR. This means that the distance from the center O to point P (on the circle) is less than the distance from the center O to point R (outside the circle).
- Thus, we can summarize that OP < OR, indicating that the distance to point R (which is outside the circle) is greater than the distance to point P (which is on the circle).
Therefore, we conclude that OP is less than OR: OP < OR.
Topper's Solved these Questions
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:EXERCISE 18 (FILL IN THE BLANKS):
Explore 5 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:A. TEST PAPER-18
Explore 8 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:C. WRITE T FOR TRUE AND F FOR FALSE FOR EACH OF THE STATEMENTS GIVEN BELOW:
Explore 1 Video
- BAR GRAPH Book:RS AGGARWALChapter:BAR GRAPH Exercise:EXERCISE
Explore 4 Videos
- CONCEPT OF PERIMETER AND AREA Book:RS AGGARWALChapter:CONCEPT OF PERIMETER AND AREA Exercise:Test Paper 21 (Fill in the Blanks)
Explore 6 Videos
Similar Questions
OP……...OQ, where O is the centre of the circle, P lies on the circle and Q is in the interior of the circle.
View SolutionDraw a circle with centre O and radius 6 cm . Mark points P, Q, R such that P lies on the circle, Q lies in the interior of the circle , and R lies in the exterior of the circle. Rewrite each of the following statements using the correct symbol (=, ⟨or⟩): OQ5 cm (ii) OP.5cm (iii) OR.5 cm
View Solution
Knowledge Check
(A) Choose the correct alternative :
O is a centre of a circle, Tangents TP and TQ of the circles itersect at point T in the exterior of the circle. Points P and Q lie on the circle . If ∠POQ=120∘ then ∠PTQ=?A120∘B30∘C60∘D90∘
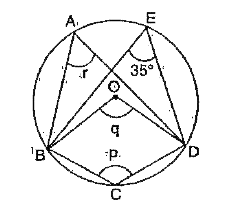
O is the centre of the circle. Find the values of p, q and r.
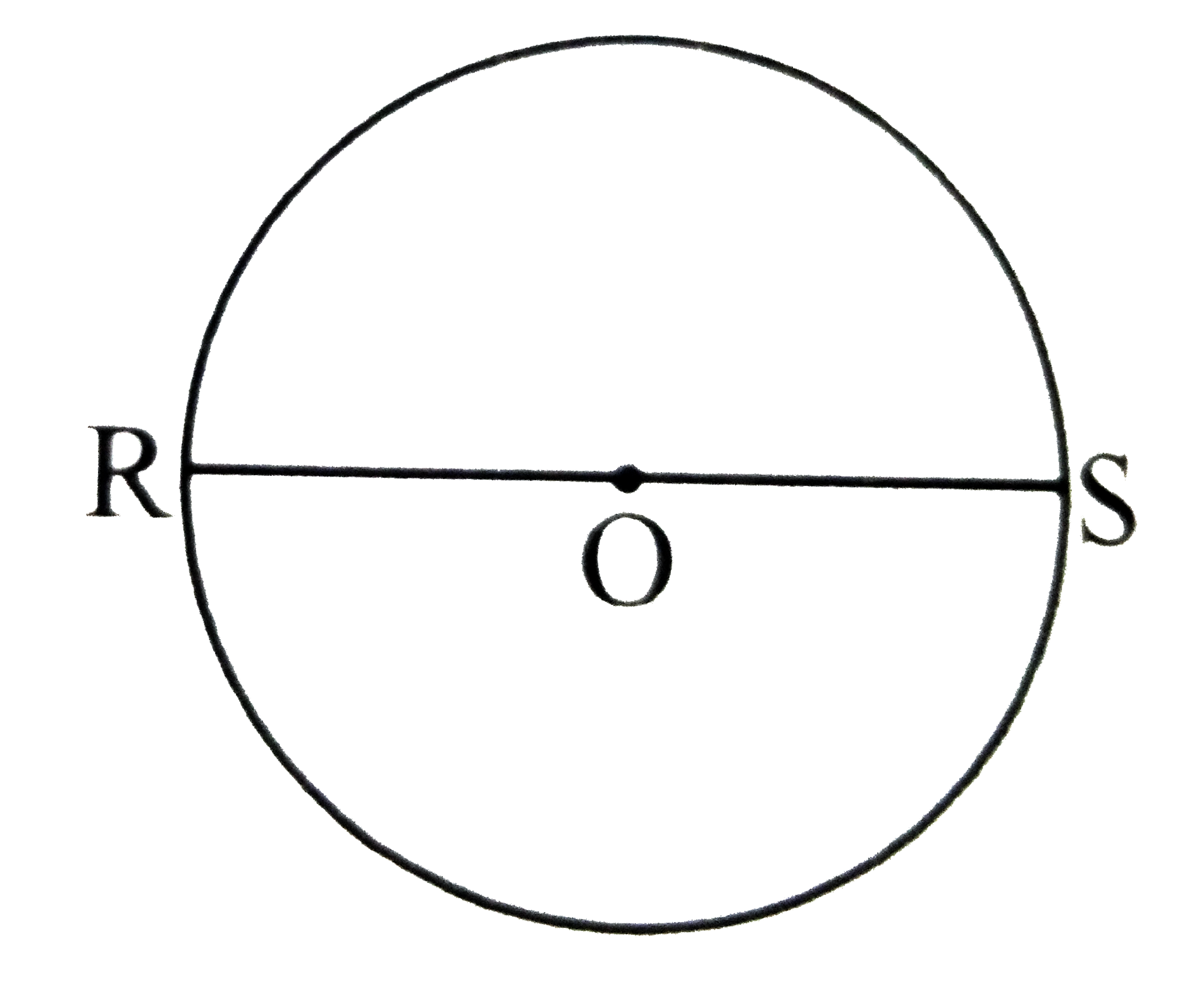
View SolutionIn the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
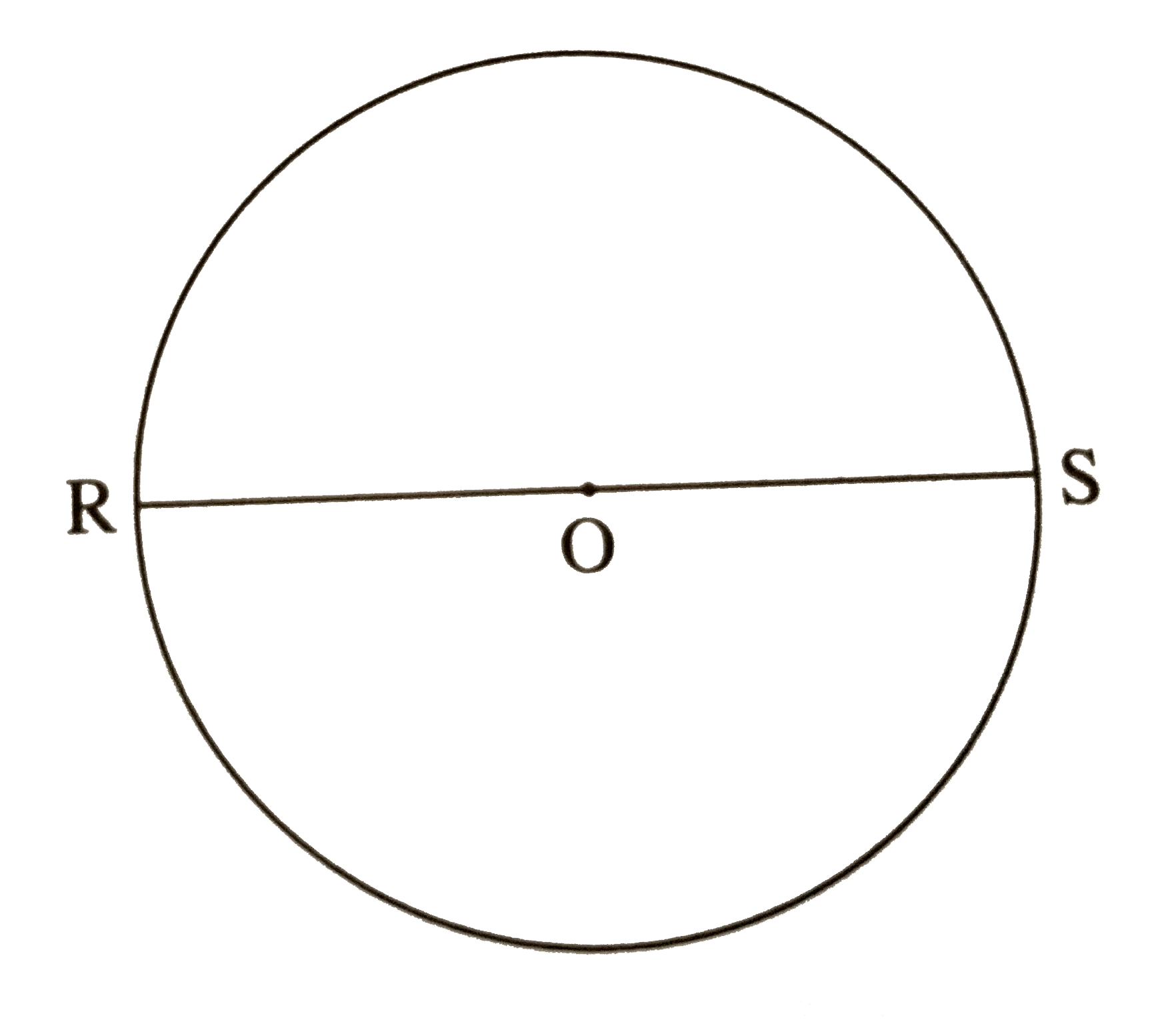
View SolutionIn figure, seg RS is a diameter of the circle with centre O. Point T lines in the exterior of the circle. Prove that ∠RTS is an acute angle.
View SolutionIf centre of the circle lies on x+y=2 and it touches the line x=3 and y=2. Find the dismeter of the circle.
View SolutionFor the four circles M, N, O and P, following four equations are given :
Circle M : x2+y2=1
Circle N : x2+y2–2x=0
Circle 0 : x2+y2−2x−2y+1=0
Circle P : x2+y2–2y=0
If the centre of circle M is joined with centre of the circle N, further centre of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
View SolutionO is the centre of the circle. OP = 5 and OT = 4, and AB = 8. The line PT is a tangent to the circle. Find PB

View SolutionIf z lies on the circle I z l = 1, then 2/z lies on
View Solution