OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
4:1
2:1
8:3
4:3
The correct Answer is:C
To solve the problem of finding the ratio of the areas of square OPQR and triangle OMN, we will follow these steps:
Step 1: Define the square and its vertices
Let the square OPQR be positioned in the coordinate plane with:
- O (0, 0) as the origin,
- P (A, 0) on the x-axis,
- Q (A, A) on the y-axis,
- R (0, A) on the y-axis.
Step 2: Identify the midpoints M and N
- M is the midpoint of side PQ. The coordinates of M can be calculated as:
M=(xP+xQ2,yP+yQ2)=(A+A2,0+A2)=(A,A2)
- N is the midpoint of side QR. The coordinates of N can be calculated as:
N=(xQ+xR2,yQ+yR2)=(A+02,A+A2)=(A2,A)
Step 3: Calculate the area of the square OPQR
The area of square OPQR is given by the formula:
Area of square=side×side=A×A=A2
Step 4: Calculate the area of triangle OMN
The area of triangle OMN can be calculated using the formula:
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Where:
- O(0,0)
- M(A,A2)
- N(A2,A)
Substituting the coordinates into the formula:
Area=12∣∣∣0(A2−A)+A(A−0)+A2(0−A2)∣∣∣
This simplifies to:
=12∣∣∣A2−A24∣∣∣=12∣∣∣4A24−A24∣∣∣=12∣∣∣3A24∣∣∣=3A28
Step 5: Find the ratio of the areas
Now, we can find the ratio of the area of the square to the area of triangle OMN:
Ratio=Area of squareArea of triangle OMN=A23A28=A2⋅83A2=83
Final Answer
The ratio of the areas of the square OPQR and triangle OMN is:
83
Let the square OPQR be positioned in the coordinate plane with:
- O (0, 0) as the origin,
- P (A, 0) on the x-axis,
- Q (A, A) on the y-axis,
- R (0, A) on the y-axis.
- M is the midpoint of side PQ. The coordinates of M can be calculated as:
M=(xP+xQ2,yP+yQ2)=(A+A2,0+A2)=(A,A2)
- N is the midpoint of side QR. The coordinates of N can be calculated as:
N=(xQ+xR2,yQ+yR2)=(A+02,A+A2)=(A2,A)
The area of square OPQR is given by the formula:
Area of square=side×side=A×A=A2
The area of triangle OMN can be calculated using the formula:
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Where:
- O(0,0)
- M(A,A2)
- N(A2,A)
Area=12∣∣∣0(A2−A)+A(A−0)+A2(0−A2)∣∣∣
This simplifies to:
=12∣∣∣A2−A24∣∣∣=12∣∣∣4A24−A24∣∣∣=12∣∣∣3A24∣∣∣=3A28
Now, we can find the ratio of the area of the square to the area of triangle OMN:
Ratio=Area of squareArea of triangle OMN=A23A28=A2⋅83A2=83
The ratio of the areas of the square OPQR and triangle OMN is:
83
Topper's Solved these Questions
- AREA OF A TRIANGLE BOOK - CENGAGECHAPTER - AREA OF A TRIANGLE EXERCISE - TEST YOURSELF (LEVEL 3 )
23 Videos
- ALGEBRAIC EXPRESSIONSBOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONSEXERCISE - TEST YOURSELF GAME TIME (Illustrated Puzzles)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - TEST YOURSELF (Multiple Choice Questions) OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
OPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
View Solution
Knowledge Check
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NMPQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
A10√2cmB20√2cmC25√2cmD15√2cm
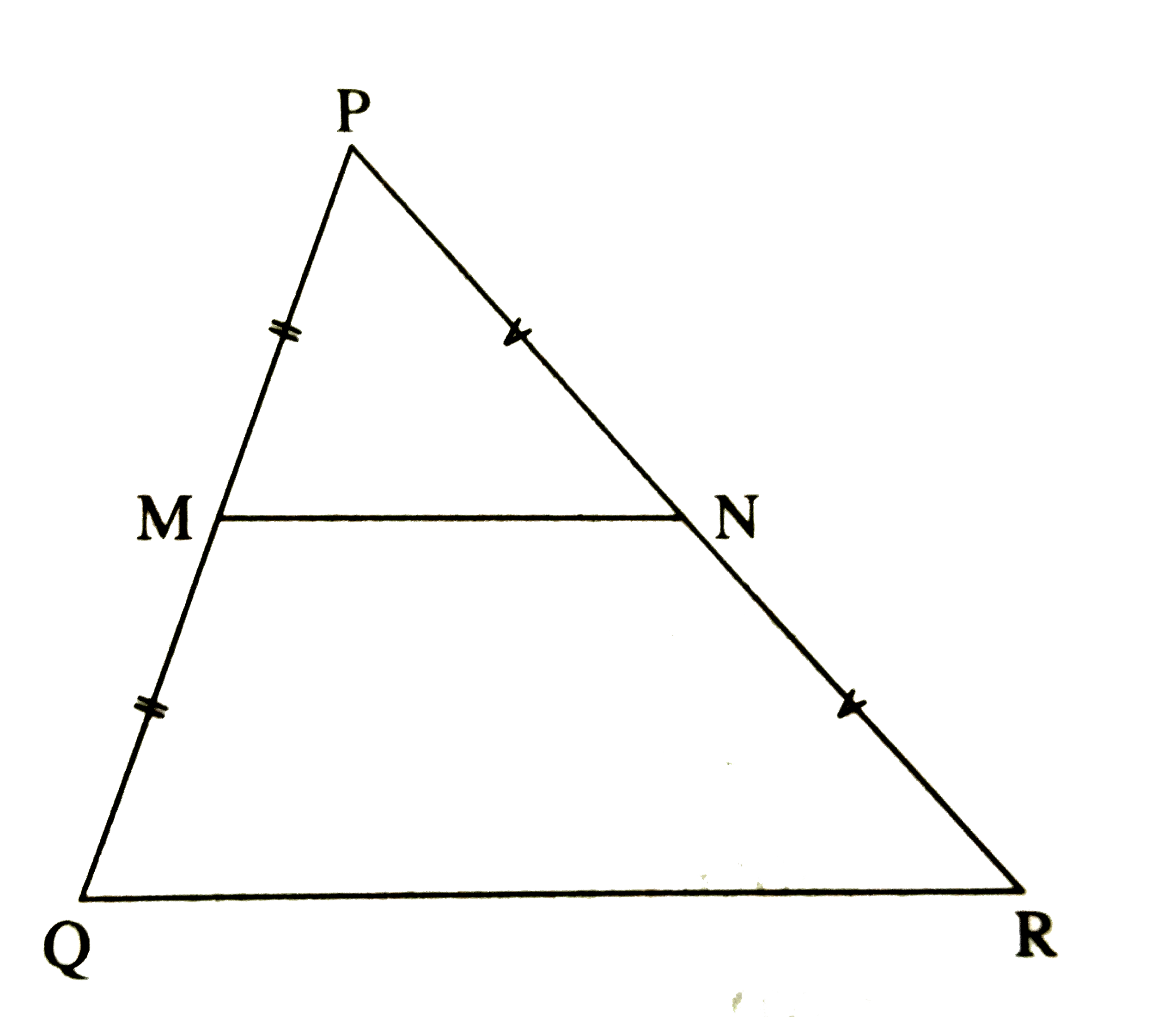
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .
View SolutionThe side of a square is 5 m and the perimeter a rectangle is equal to the perimeter of the square. If the length of the rectangle is 6 m, then find the ratio of the areas of the square and the triangle.
View SolutionIn a square PQRS, X and Y are mid points of sides PS and QR respectively. XY and QS intersect a t O. Find the area of ΔXOS, if PQ = 8 cm.
View SolutionThe radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
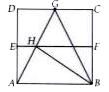
View SolutionIn the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
View Solution
