Out of 3n consecutive integers, three are selected at random. Find the probability that their sum is divisible by 3.Solution in Bengali
Out of 3n consecutive integers, n integers will be of 3k type, n integers will be of 3k + 1 type and n integers will be of 3k + 2 type.
If sum of three integers selected is divisible by 3, then we have following possibilities.
All integers are of same type.
∴ Number of ways of selection = .nC3+.nC3+.nC3=3×.nC3
One integer of each type.
∴ Number of ways of selection = .nC1×.nC1×.nC1=n3
So, number of favourable ways = 3×.nC3+n3
Total number of ways = .3nC3
∴ Required probability = 3×.nC3+n3.3nC3=3n2−3n+2(3n−1)(3n−2)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Solved Example9videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions470videos
PROBABILITY
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
Similar Questions
When a fair dice is rolled, the number that comes up top is a number between one to six. Assuming we roll the dice once, to check the possibility of three coming up.
07:31View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
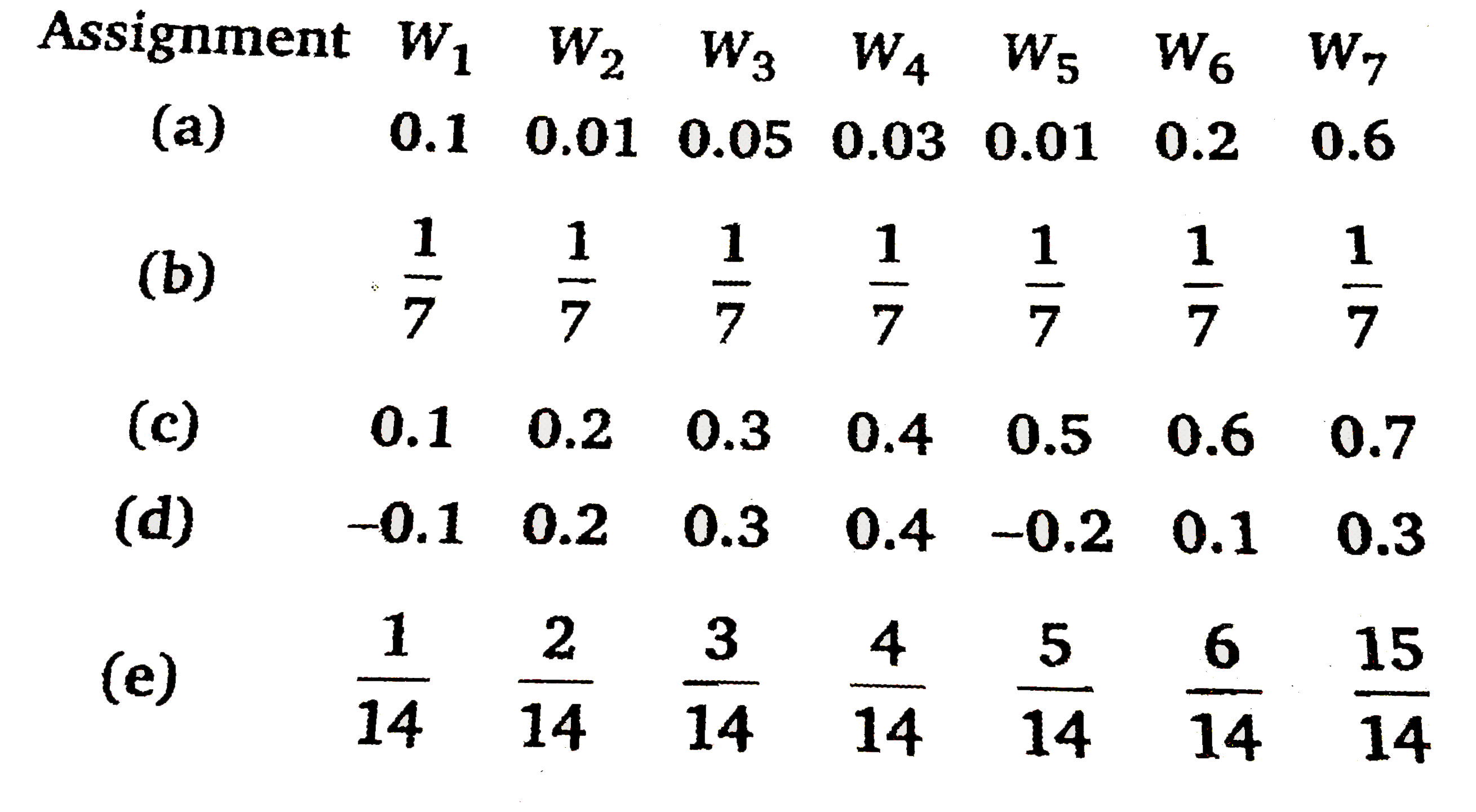 04:28View Solution
04:28View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
06:55View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
04:56View SolutionOut of 3n consecutive integers, there are selected at random. Find the probability that their sum is divisible by 3.
07:37View SolutionOut of 40 consecutive integers,two are chosen at random,the probability that their sum is odd is
04:48View SolutionOut of 3n consecutive natural numbers, 3 natural numbers are chosen at random without replacement. The probability that the sum of the chosen numbers is divisible by 3, is
03:38View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
06:01View SolutionOut of 30 consecutive integers, three integers are drawn at random. Find the probability that their sum is (i) an odd number (ii) an even number
03:34View SolutionOut of 3n consecutive integers, three are selected at random. Show that the chance that their sum is divisible by 3 is 3n2−3n+2(3n−1)(3n−2)
02:52View SolutionOut of 3n consecutive integers, there are selected at random. Find the probability that their sum is divisible by 3.
02:49View SolutionOut of 3n consecutive integers, three are selected at random. Find the probability that their sum is divisible by 3.
06:43View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
06:17View SolutionOut of 3 n consecutive integers, three are selected at random. Find the probability that their sum is divisible by 3 is
09:34View SolutionOut of 40 consecutive integers, two are chosen at random, the probability that their sum is odd is
11:48View SolutionOut of 3n consecutive integers, there are selected at random. Find the probability that their sum is divisible by 3.
06:25View Solution

