over the towers of a bridge a cable is hung in the form of a parabola, have their tops 30 meters above the road way are 200 meters apart. If the cable is 5 meters above the road way at the centre of the bridge, then the length of the vertical supporting cable 30 meters from the centre is
Let us assume that lowest point of cable as origin and equation of parabola will be x2=4ay
Given, tower of bridge is 30 meters above the road-way and lowest point is 5 meters above the road.
Then in equation y-coordinate of top of tower is 25 meters and x-coordinate is 100 meters,
from equation we get 1002=4a(25)
⇒a=100
Now,length of the vertical supporting cable 30 metres from the centre is given by y+5 where y is given by 302=4(100)(y)
⇒y=94
Then vertical length of cable is 5+94=294
.
Topper's Solved these Questions
Similar Questions
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground lenvel and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown i fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? Explain.

View SolutionThe cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
View Solution
Knowledge Check
Each side of an equilateral triangle subtends an angle of 60∘ at the top of a tower h meters high located at the centre of the triangle. If a meters is the length of each side of the triangle, then
A3a2=2h2B2a2=3h2Ca2=3h2D3a2=h2A man whose eye leave is 1.5 meters above the ground observes the angle of elevation of the tower to be 60∘. If the distance of the man from the tower be 10 meters, the height of the tower is
A(1.5+10√3)B10√3mC(1.5+10√3)mDNone of theseEach side of an equilateral triangle subtends an angle of 60∘ at the top a tower h meter high located at the centre of the triangle. If a is the length of each side of the triangle, then
A3a2=2h2B2a2=3h2Ca2=3h2D3a2=h2
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
View SolutionIF the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
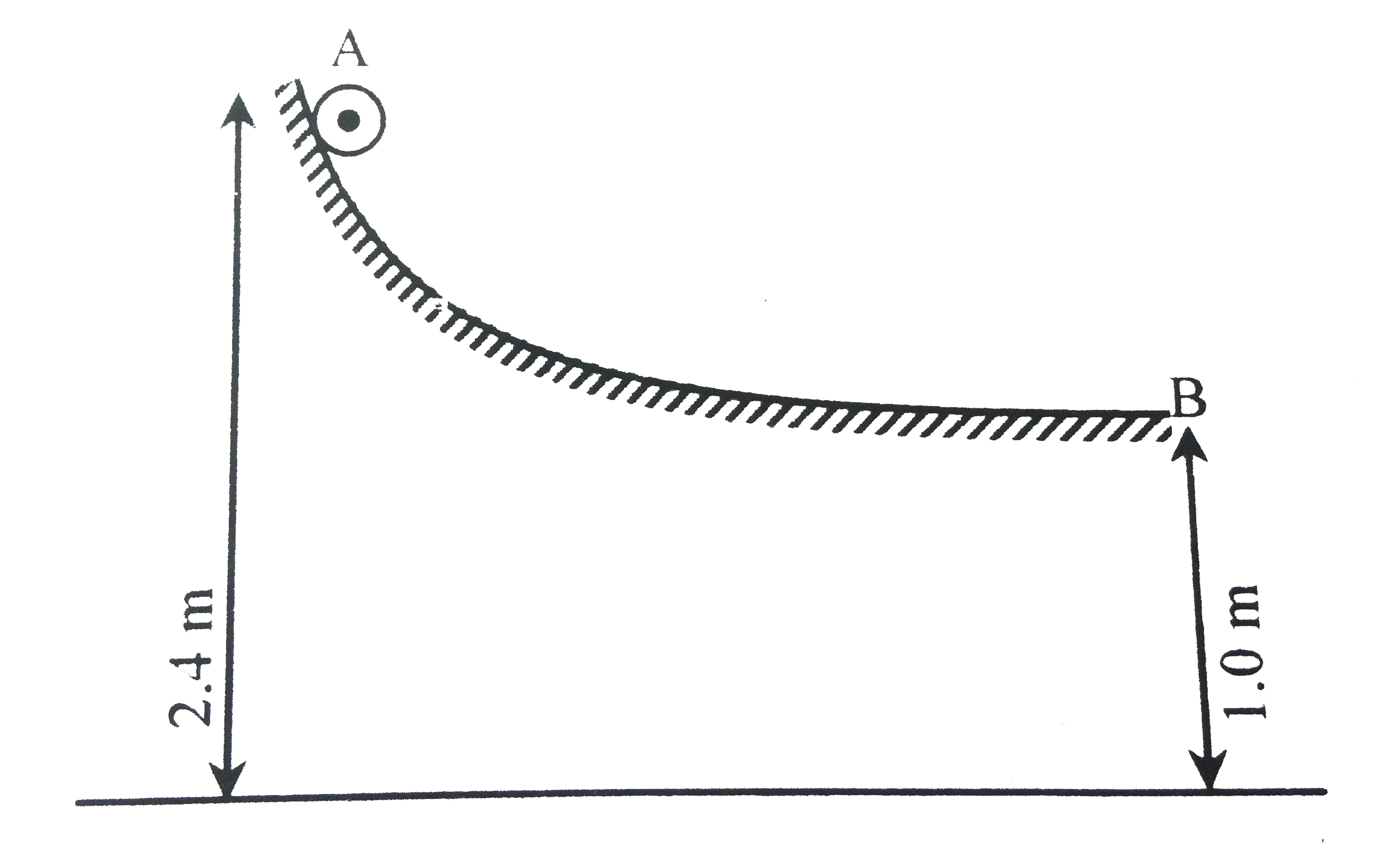 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionA nail is driven into the trunk of a 30 year old tree at a point 1 meter above the soil level. The tree grown in height at the rate pf 0.5 meters a year After three years, the nail will be
View SolutionIf from the top of a tower 80 meters high the angles of depression of the top and bottom of a house are 30∘and45∘ respectively, then the height of the house is
View Solution
