P and Q are the points on the sides DE and DF of a triangle DEF such that DP = 5 cm, DE = 15 cm, DQ = 6 cm and QF = 18 cm. Is PQ||EF? Give reasons for your answer
The correct Answer is:DPPE≠DQQF
To determine whether line segment PQ is parallel to line segment EF in triangle DEF, we will use the Basic Proportionality Theorem (also known as Thales' theorem). According to this theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Measurements:
- DP = 5 cm
- DE = 15 cm
- DQ = 6 cm
- QF = 18 cm
2. Calculate the Remaining Lengths:
- Since DE = 15 cm and DP = 5 cm, we can find PE (the remaining length):
PE=DE−DP=15cm−5cm=10cm
3. Set Up the Proportions:
- According to the Basic Proportionality Theorem, if PQ is parallel to EF, then:
DQQF=DPPE
4. Substitute the Values:
- Substitute the known values into the proportion:
DQQF=618andDPPE=510
5. Simplify the Ratios:
- Simplifying the left side:
618=13
- Simplifying the right side:
510=12
6. Compare the Ratios:
- Now we compare the two ratios:
13≠12
7. Conclusion:
- Since the ratios are not equal, we conclude that:
PQ is not parallel to EF.
- DP = 5 cm
- DE = 15 cm
- DQ = 6 cm
- QF = 18 cm
- Since DE = 15 cm and DP = 5 cm, we can find PE (the remaining length):
PE=DE−DP=15cm−5cm=10cm
- According to the Basic Proportionality Theorem, if PQ is parallel to EF, then:
DQQF=DPPE
- Substitute the known values into the proportion:
DQQF=618andDPPE=510
- Simplifying the left side:
618=13
- Simplifying the right side:
510=12
- Now we compare the two ratios:
13≠12
- Since the ratios are not equal, we conclude that:
PQ is not parallel to EF.
Topper's Solved these Questions
- MID TERM TEST PAPER BOOK - VK GLOBAL PUBLICATIONCHAPTER - MID TERM TEST PAPER EXERCISE - SECTION -C
10 Videos
- MID TERM TEST PAPER BOOK - VK GLOBAL PUBLICATIONCHAPTER - MID TERM TEST PAPER EXERCISE - SECTION -D
7 Videos
- MID TERM TEST PAPER BOOK - VK GLOBAL PUBLICATIONCHAPTER - MID TERM TEST PAPER EXERCISE - SECTION -D
7 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - VK GLOBAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - SELF - ASSESSMENT TEST
9 Videos
- MODEL QUESTION PAPER - 1 BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 1 EXERCISE - SECTION - C
15 Videos
Similar Questions
L and M are respectively the points on the sides DE and DF of a triangle DEF, such that DL = 4, LE=43,DM=6 and DF=8. Is Lm||EF? Give reason.
View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
View Solution
Knowledge Check
In figure ,DE||BC in triangle ABC such that BC = 8 cm , AB = 6 cm and DA = 1.5 cm .find DE.
 A2 cmB3 cmC4 cmD5 cm
A2 cmB3 cmC4 cmD5 cmIn ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cm
R and S are points on the sides DE and EF respectively fo a △DEF such that ER = 5 cm, RD=2.5cm,SE=1.5cm and FS=3.5cm. Find Whether RS∣∣DF or not.
View SolutionR and s are points on the sides DE and EF respectively of a ΔDEF such that ER = 5 cm , RD = 2.5 cm , SE = 1.5 cm and FS = 3.5 cm .Find whether RS||DF or not .
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AD=2cm, BD=3cm,BC=7.5cm and DE || BC. Then length of DE (in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AE = 5 cm, AC= 7.5 cm, DE= 4.2 cm and DE||BC. Then find length of BC.
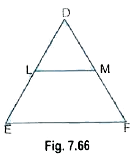
View SolutionL and M are points on the sides DE and DF respectively of a MJEF. State whether LM II EF or not.
DE = 8 cm, DF = 15 cm, LE = 3.2 cm and MF= 6 cm.
View Solution△ABC−△DEF such that DE=3cm,EF=2cm,DF=2.5cm and BC=4cm. Find perimeter of △ABC.
View Solution
