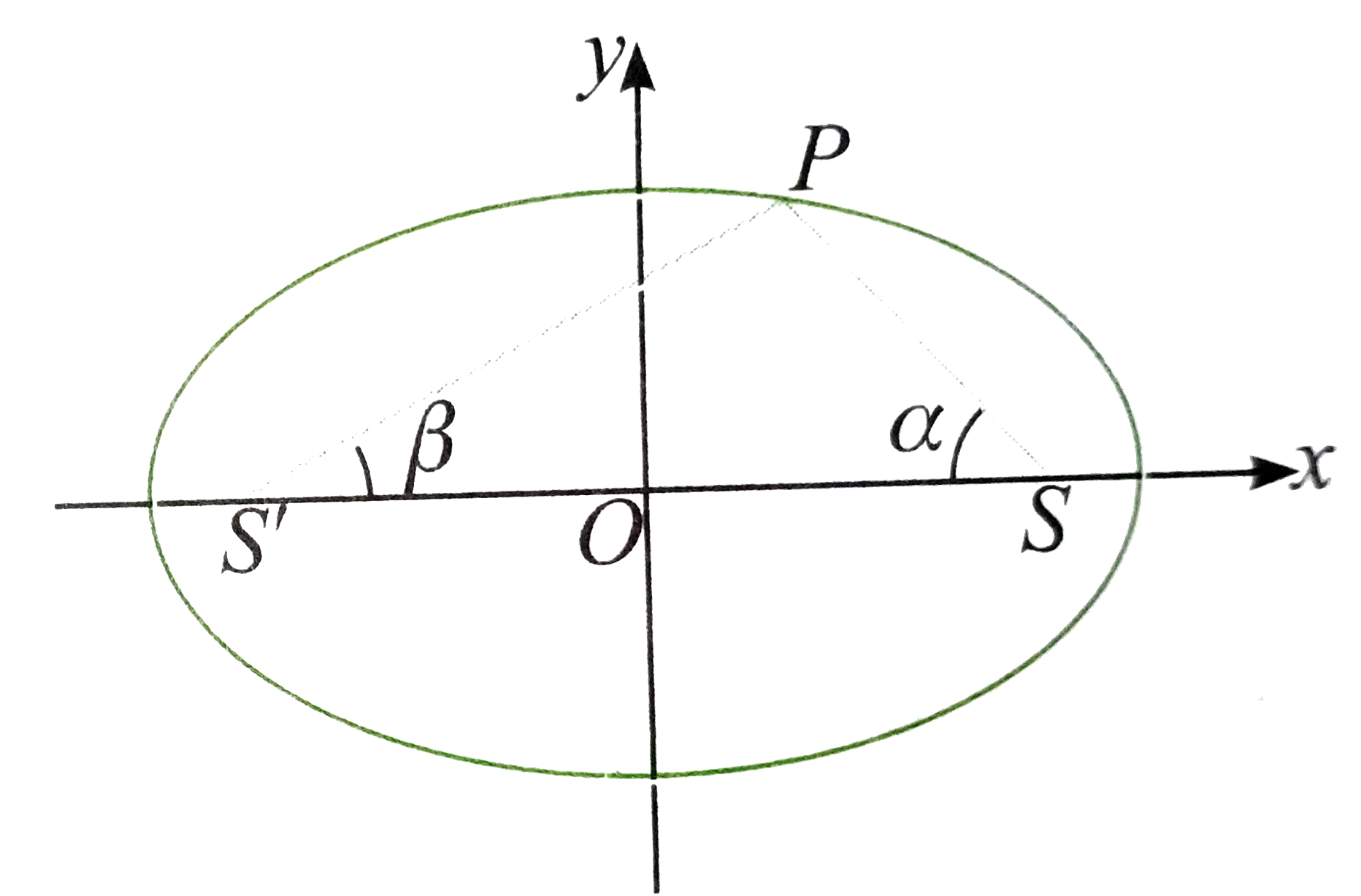
P is any point lying on the ellipse x2a2+y2b2=1(a>b) whose foci are S and S'. If ∠PSS'=aand∠PS'S=β, then the value of tan.α2tan.β2 is
A
1+e1−e
B
1+e21−e2
C
1−e1+e
D
1
Video Solution
Text Solution
The correct Answer is:C
SP+S''P=2a
In ΔSPS''
Perimeter, 2s=SP+S'P+SS'=2a+2ae=2a(1+e)
Now, tan.α2tan.β2=√(s−b)(s−c)s(s−c)√(s−a)(s−c)s(s−b)
s−cs=2s−2c2s=2a(1+e)−2c2a(1+e)
2a+2ae−4ae2a(1+e)=2a(1−e)2ae(1+e)
∴tan.α2tan.β2=1−e1+e
|
Similar Questions
Knowledge Check
If P is any point on the ellipse x225+y29=1 whose foci are S and S' perimeter of ΔSPS' is
A18B50C34D9If P is a point on the ellipse X29+y24=1
whose foci are S and S' then the value of PS + PS' isA6B4C3D2If P is a point on the ellipse x216+y225=1 whose foci are S and S', then PS+PS'=8.
A6B8C10D12
If P(α,β) is a point on the ellipse x2a2+y2b2=1 with foci SandS' and eccentricity e, then prove that the area of SPS' is ba√a2−α2
View SolutionIf 3sinα=sinβ≠0, then the value of ∣∣ ∣ ∣∣tan(α+β2)tan(α−β2)∣∣ ∣ ∣∣
View SolutionIf 3sinα−sinβ≠0, then the value of ∣∣ ∣ ∣∣tan(α+β2)tan(α−β2)∣∣ ∣ ∣∣
View SolutionIf the chord joining points P(α)andQ(β) on the ellipse (x2a2)+(y2b2)=1 subtends a right angle at the vertex A(a,0), then prove that tan(a2)tan(β2)=−b2a2.
View SolutionIf P is any point on the ellipse 9x2+36y2=324 whose foci are S and S'. Then, SP + S' P equals
View Solution