P is any point lying on the ellipse x2a2+y2b2=1(a>b) whose foci are S and S'. If ∠PSS'=αand∠PS'S=β, then the value of tan.α2tan.β2 is Solution in Tamil
1+e1−e
1+e21−e2
1−e1+e
1
The correct Answer is:C
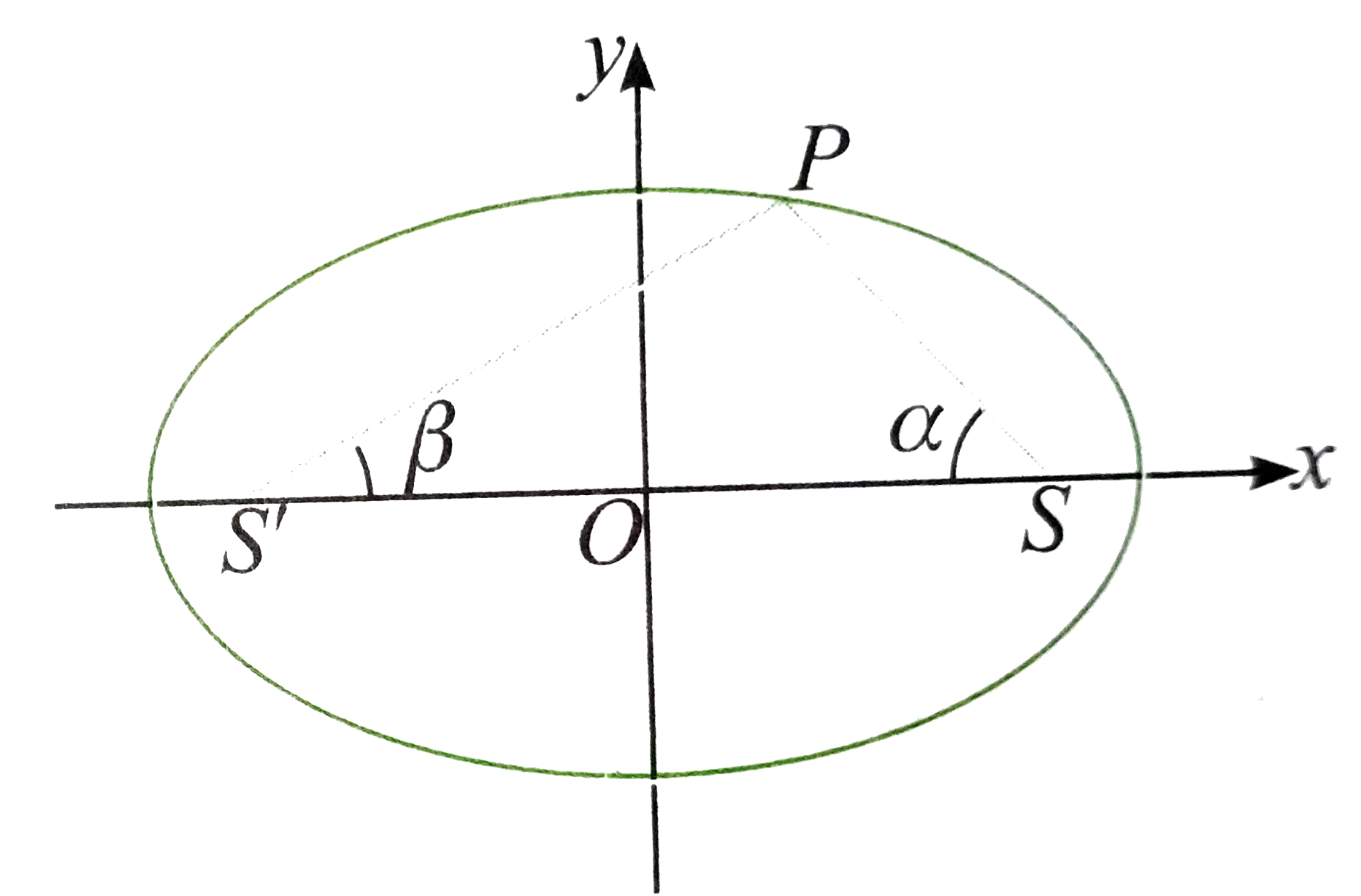
SP+S''P=2a
In ΔSPS''
Perimeter, 2s=SP+S'P+SS'=2a+2ae=2a(1+e)
Now, tan.α2tan.β2=√(s−b)(s−c)s(s−c)√(s−a)(s−c)s(s−b)
s−cs=2s−2c2s=2a(1+e)−2c2a(1+e)
2a+2ae−4ae2a(1+e)=2a(1−e)2ae(1+e)
∴tan.α2tan.β2=1−e1+e
Similar Questions
If S,S' be the foci of an ellipse and p be any point on it show that tan(12)∠PSS'×tan(12)∠PS'S=1−e1+e
View SolutionP and Q are the points on the ellipse "3x2+4y2=12" with eccentric angles "α" and "β" respectively and whose foci are at "S and S" .If "PS" and "QS'" are parallel than "tan(α)2tan(β)2" can
View Solutiontan2α+2tanαtan2β=tan2β+2tanβtan2α হলে দেখাও যে হয়, tanβ=±tanα
View SolutionIf α+β+γ=2π, then (a) tan(α2)+tan(β2)+tan(γ2)=tan(α2)tan(β2)tan(γ2) (b)tan(α2)tan(β2)+tan(β2)tan(γ2)+tan(γ2)tan(α2)=1 (c)tan(α2)+tan(β2)+tan(γ2)=−tan(α2)tan(β2)tan(γ2) (d)none of these
View SolutionP is any point lying on the ellipse x2a2+y2b2=1(a>b) whose foci are S and S'. If ∠PSS'=αand∠PS'S=β, then the value of tan.α2tan.β2 is
View Solutionयदि P दीर्घवृत्त x2a2+y2b2=1 का एक बिन्दु है जिसकी नाभियाँ S तथा S' है यदि ∠PSS'=α तथा ∠PS'S=β है, तो
View SolutionIf P is any point lying on the ellipse x2a2+y2b2=1 , whose foci are SandS'. Let ∠PSS'=αand∠PS'S=β ,then
View SolutionIf α+β+γ=2π, then (a) tan(α2)+tan(β2)+tan(γ2)=tan(α2)tan(β2)tan(γ2) (b)tan(α2)tan(β2)+tan(β2)tan(γ2)+tan(γ2)tan(α2)=1 (c)tan(α2)+tan(β2)+tan(γ2)=−tan(α2)tan(β2)tan(γ2) (d)none of these
View Solution
