P is point in the interior of ABC as shown in fig.47.states which of the following statements are true (T) or false (F): AP+PB<AB (ii) AP+PC>AC BP+PC=BC
To solve the problem, we need to analyze the statements given in relation to point P, which lies inside triangle ABC. We will use the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
1. Evaluate Statement (i): AP+PB<AB
- According to the triangle inequality theorem, for triangle APB, we have:
AP+PB>AB
- Therefore, the statement AP+PB<AB is False (F).
2. Evaluate Statement (ii): AP+PC>AC
- For triangle APC, the triangle inequality theorem states:
AP+PC>AC
- This aligns with the statement given, so AP+PC>AC is True (T).
3. Evaluate Statement (iii): BP+PC=BC
- For triangle BPC, the triangle inequality theorem states:
BP+PC>BC
- Since the statement claims equality, BP+PC=BC is False (F).
Summary of Results:
- (i) AP+PB<AB → False (F)
- (ii) AP+PC>AC → True (T)
- (iii) BP+PC=BC → False (F)
AP+PB>AB
- Therefore, the statement AP+PB<AB is False (F).
AP+PC>AC
- This aligns with the statement given, so AP+PC>AC is True (T).
BP+PC>BC
- Since the statement claims equality, BP+PC=BC is False (F).
- (i) AP+PB<AB → False (F)
- (ii) AP+PC>AC → True (T)
- (iii) BP+PC=BC → False (F)
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One or More
If a,b,c are in H.P. then which of the following is true.
Aa1−2a,b1−2b,c1−2c are in H.P.Bln(a−b2),ln(b)2,ln(c−b2) are in H.P.Cc−b2,b2,a−b2 are in G.P.De2/a,e1/b,e1/c are in G.P. - Question 2 - Select One
If a,b,c are in A.P. b, c,d are in G.P. and c,d,e are in H.P., then which one of the following is true :
A2c=a+eBae=c2Cc=2aea+eDab=de
If ABC≅PQR and ABC is not congruent to RPQ, then which of the following not true: BC=PQ (b) AC=PR (c) AB=PQ (D) QR=BC
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
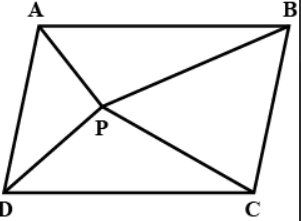 View Solution
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
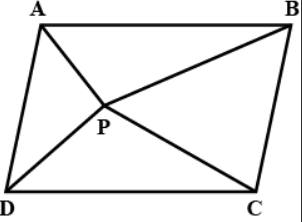 View Solution
View SolutionIf a, b, c are in G.P. that the following are also in G.P.
√a,√b,√c are in G.PView SolutionIf p is any statement, t and c are a tautology and a contradiction respectively then which of the following is not correct- (a) p∧t=p (b) p∧c=c (c) p∨t=c (d) p∨c=p
View SolutionIn Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
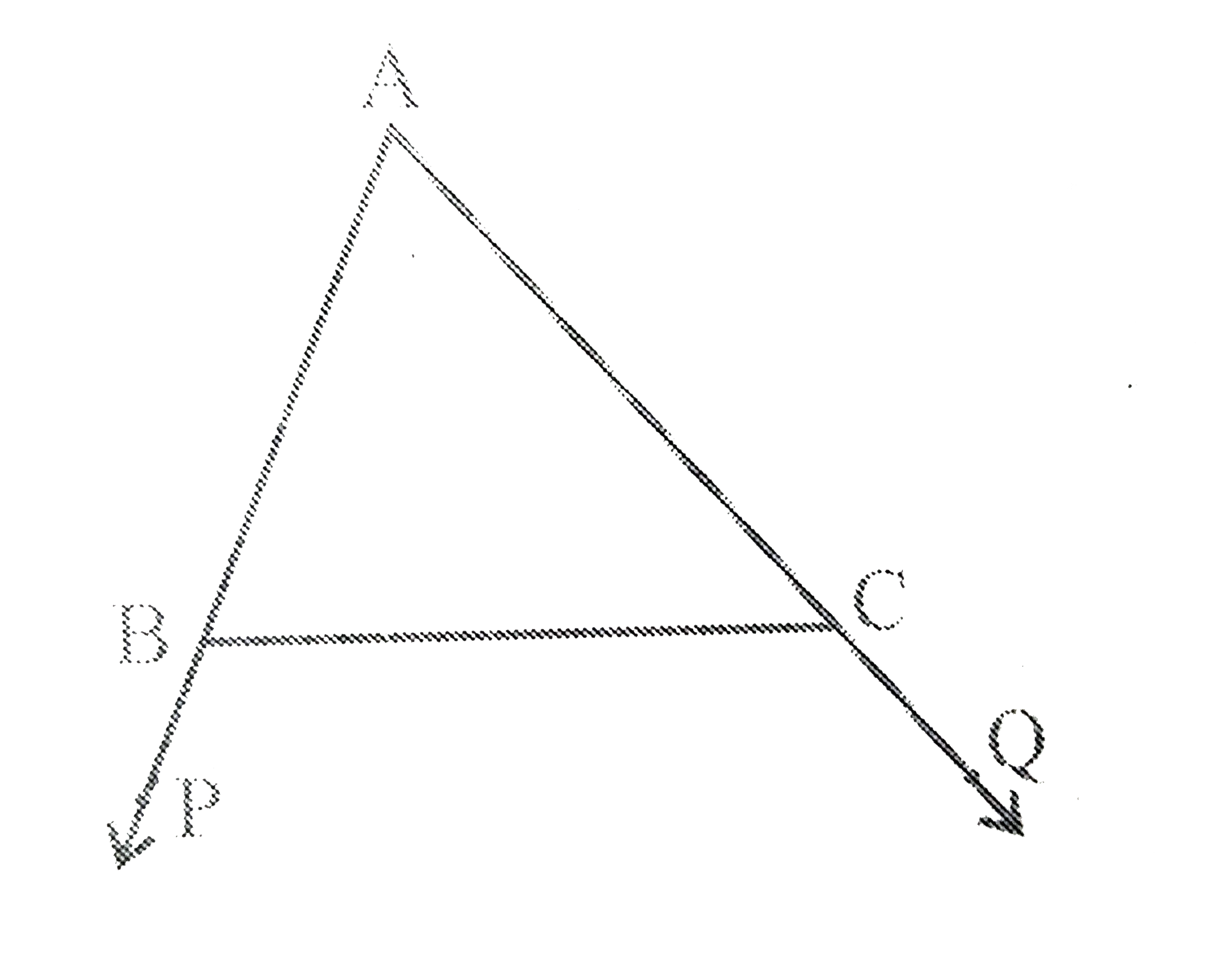 View Solution
View Solution

