P is the variable point on the circle with center at C.CA and CB are perpendiculars from C on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle PAB is a circle with center at the centroid of triangle CAB and radius equal to the one-third of the radius of the given circle.Solution in Tamil
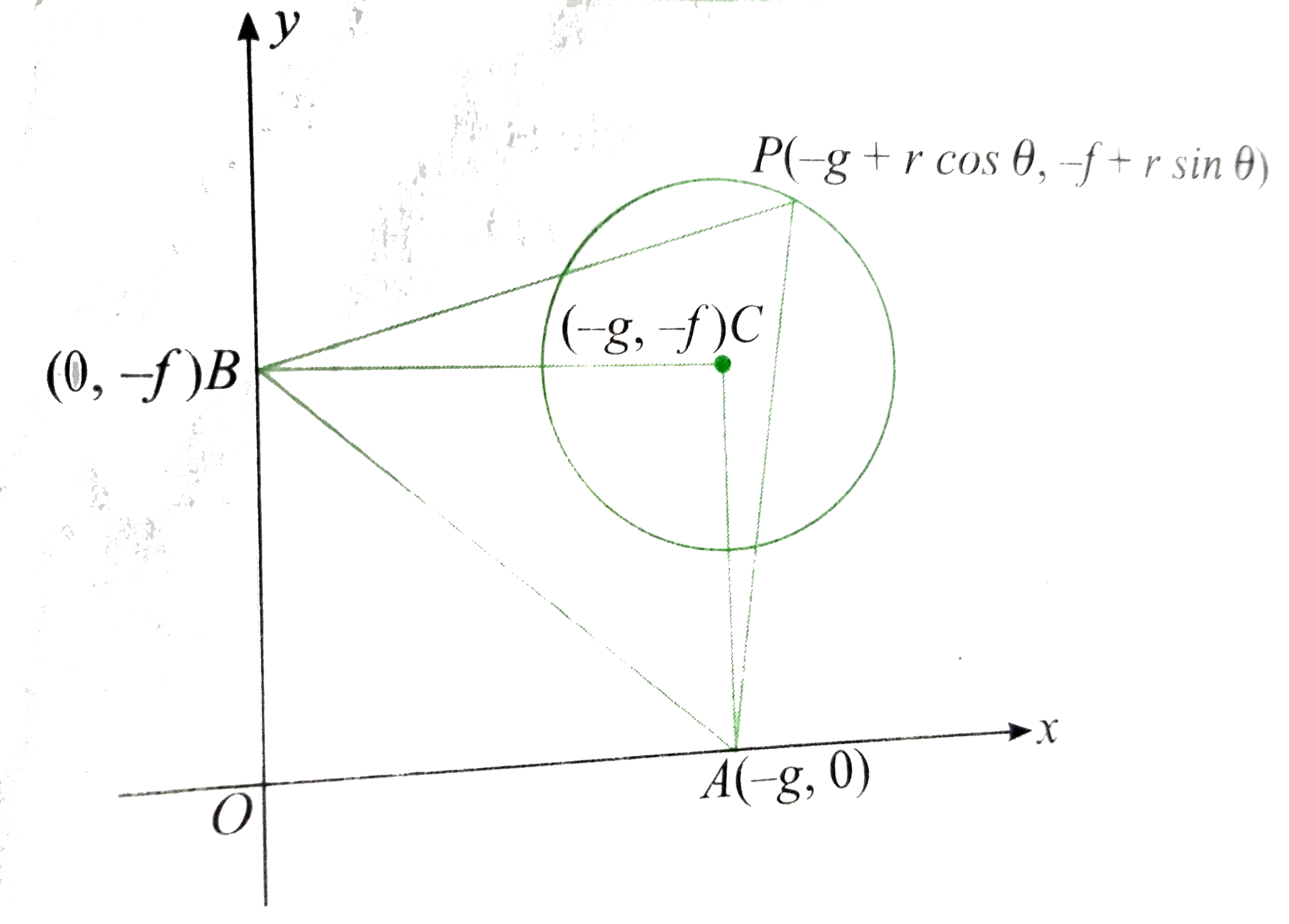
Let the circle be x2+y2+2gx+2fy+c=0.
Let the centroid of triangle PAB be (h,k). ltBRgt ∴3h=2g+rcosθ
and 3k=−2f+rsinθ
⇒(2h+2g)2+(3k+2f)2=r2
⇒(x+2g/3)2+(y+2/3)2=r2/9
This is the required locus which is a circle.
Centre of the circle is (−2g/3,−2f/3) which is centroid of the triangle CAB and radius (r/3) which is one-third of the radius of the given circle.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
06:15View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
03:21View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:27View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:06View SolutionP is the variable point on the circle with center at C.CA and CB are perpendiculars from C on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle PAB is a circle with center at the centroid of triangle CAB and radius equal to the one-third of the radius of the given circle.
05:06View SolutionA circle of radius 'r' passes through the origin O and cuts the axes at A and B, Locus of the centroid of triangle OAB is
05:00View SolutionA variable plane is at a constant distance p from the origin and meets the axes in A, B and C. The locus of the centroid of the triangle ABC is
06:32View SolutionA circle of radius 3k passes through (0.0) and cuts the axes in A and B then the locus of centroid of triangle OAB is
02:59View Solutioncircle of radius 3k passes through (0,0) and cuts the axes in A and B then the locus of centroid of triangle OAB is
02:38View Solutionमाना एक त्रिभुज का लम्ब केन्द्र तथा केन्द्रक क्रमशः A (-3,5) तथा B(3,3) हैं। यदि इस त्रिभुज का परिकेन्द्र C है, तो रेखाखण्ड AC को व्यास मान कर बनाए जाने वाले वृत्त की त्रिज्या है
06:22View SolutionOrthocentre and centroid of a triangle are A(-3,5) and B(3,3) respectively. If C is the circumcentre and AC is the diameter of this circle, then find the radius of the circle.
05:23View SolutionNews x^(2) + y^(2) = 25 That a chord moves the right angle at the center of the circle. The variable point on the chord and circle is the locus of the centroid of the triangle formed by P.
09:01View SolutionThe centres of the circles are (a, c) and (b, c) and their radical axis is y-axis. The radius of one of the circles is r. The radius of the other circle is
04:50View SolutionP is the variable point on the circle with center at C.CA and CB are perpendiculars from C on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle PAB is a circle with center at the centroid of triangle CAB and radius equal to the one-third of the radius of the given circle.
05:12View SolutionA circle of radius 'r' passes through the origin O and cuts the axes at A and B,Locus of the centroid of triangle OAB is
05:27View SolutionLet the orthocentre and centroid of a triangle be A(−3,5)andB(3,3) respectively. If C is the circumcentre of the triangle then the radius of the circle having line segment AC as diameter, is
06:42View Solution

