(p∧~q)∧(~p∨q) is
A
a tautology
B
a contradiction
C
both a tauology and a contradiction
D
neither a tauology nor a contradiction
Video Solution
Text Solution
The correct Answer is:B
The truth table of (p∧~q)∧(~p∨q) is a given below:

The last column of the above truth table contains F only . So, the given statement is a contradiction.
|
Topper's Solved these Questions
- MATHEMATICAL REASONING Book:OBJECTIVE RD SHARMAChapter:MATHEMATICAL REASONING Exercise:Section II - Assertion Reason Type
Explore 4 Videos
- MATHEMATICAL REASONING Book:OBJECTIVE RD SHARMAChapter:MATHEMATICAL REASONING Exercise:Exercise
Explore 40 Videos
- MATHEMATICAL REASONING Book:OBJECTIVE RD SHARMAChapter:MATHEMATICAL REASONING Exercise:Solved MCQs
Explore 5 Videos
- MATHEMATICAL INDUCTION Book:OBJECTIVE RD SHARMAChapter:MATHEMATICAL INDUCTION Exercise:Exercise
Explore 30 Videos
- MAXIMA AND MINIMA Book:OBJECTIVE RD SHARMAChapter:MAXIMA AND MINIMA Exercise:Chapter Test
Explore 30 Videos
Similar Questions
Knowledge Check
Negation of (~p∧~q)∨(~p∨r) is
A(p∨q)∧(p∧~r)B(p∧q)∨(p∧~r)C(p∧q)∧(p∧~r)D(p∨q)∨(p∧~r)~[(p∧q)→(~p∨q)] is a
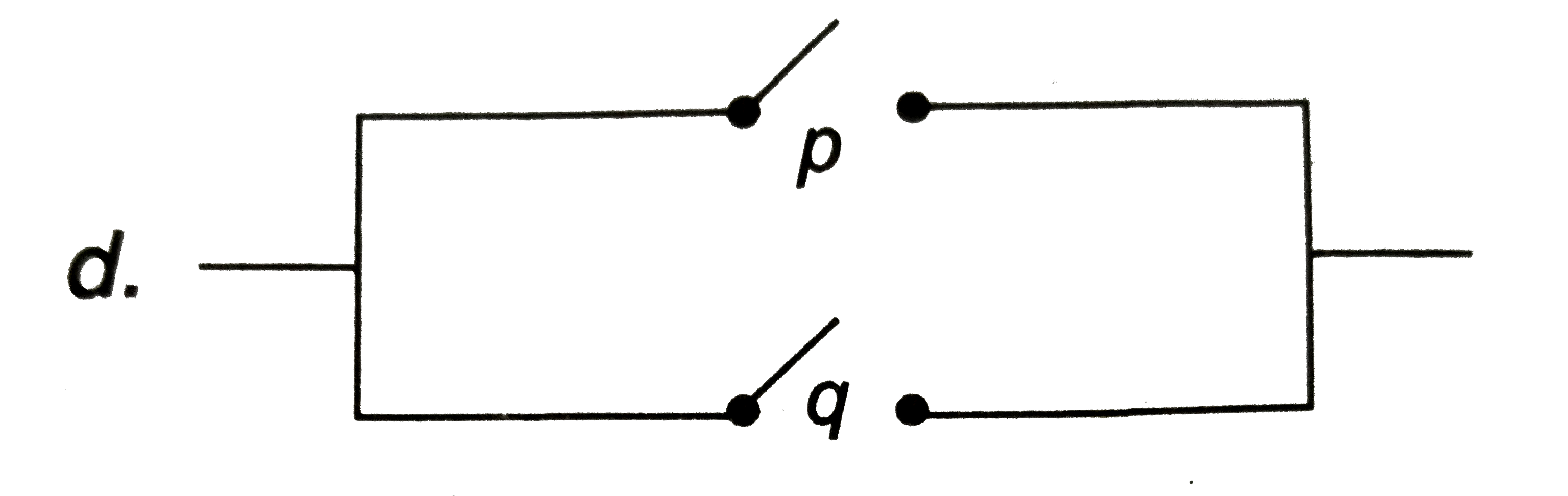
AtautologyBcontradictionCNeither (a) nor (b)DEither (a) or (b)Quivalent circuit for the logical expression (~p∧q)∨(~p∧~q)∨(p∧~q) is
A B
B C
C D
D