PARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
x+y=4
(x−4)2+(y−4)2=16
(x−4)(y−4)=4
xy=4
The correct Answer is:A
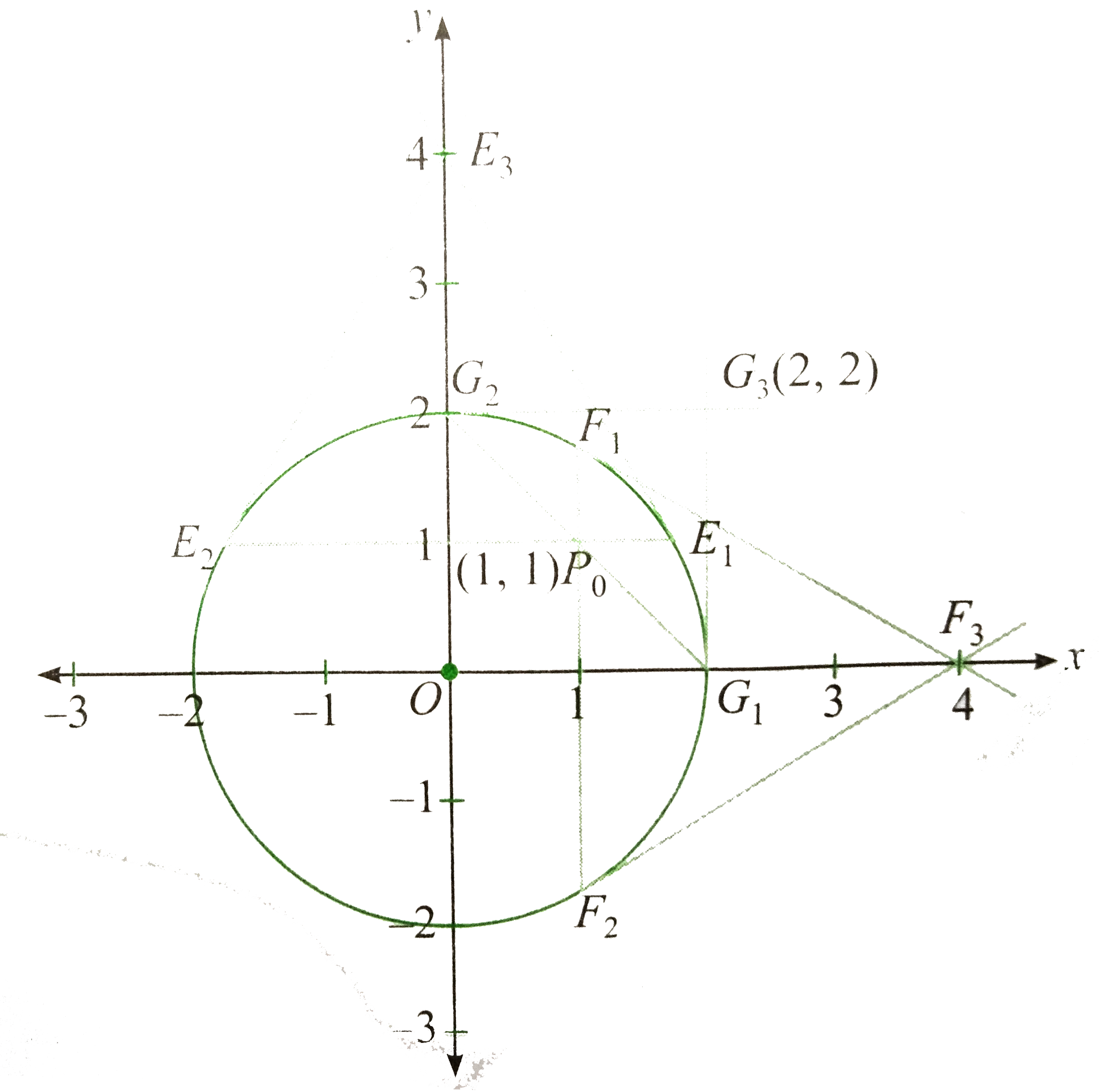
Circle is x2+y2=4.
Equation of chord through P0(1,1) parallel to x-axis is y=1
Solving this with circle, we E1(√3,1) and E2(−√3,1).
Equations of tangent to circle at E1 and E2 are √3x+y=4 and −√3x+y=4 , respectively.
These tangents meet at E3(0,4).
Chord through p0(1,1), parallel to y -axis is x=1, which meets circle at F1(1,√3) and F2(1,−√3).
Tangents to circle at F1 and F2 meet at F3(0,4).
Chord through P0 having slope -1 is x+y=2 which meets circle at G1(0,2) and G2(2,0).
Tangest to circle at G1 and G2 meet at G3(2,2).
Clearly, E3,F3 and G3 lie on line x+y=4.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - LINKED COMPREHENSION TYPE (For problem 1 and 2)
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Let the equation of a curve passing through the point (0,1) be given b y=∫x2ex3dx. If the equation of the curve is written in the form x=f(y), then f(y) is
View SolutionLet C be a curve defined by y=ea+bx2. The curve C passes through the point P(1,1) and the slope of the tangent at P is (−2). Then the value of 2a−3b is_____.
View Solution
Knowledge Check
Let E1E2andF1F2 be the chords of S passing through the point P∘ (1, 1) and parallel to the X-axis and the Y-axis, respectively. Let G1G2 be the chord of S passing through P∘ and having slope -1. Let the tangents to S at E1andE2 met at F3, and the tangents to S at G1andG2 meet at G3. Then , the points E3,F3andG3 lie on the curve
Let S be the circle in the XY-plane defined by the equation
x2+y2=4Ax + y = 4B(x−4)2+(y−4)2=16C(x−4)+(y−4)=4Dxy = 4A tangent to the curve. Y=f(x) at P(x, y) meets x-axis at A and y-axis at B. If AP:BP=1:3 and f(1)=1, then the curve also passes through the point
A(13,24)B(12,4)C(2,18)D(3,18)The slope of the tangent to a cruve y=f(x) at (x,f(x)0 is 2x+1.If the curve passes through the point (1,2) then the area of the region bounded by the curve,the x-axis and the lien x=1 is
A56 sq. unitsB65 sq.unitsC16 sq. unitsD6 sq. units
Let E1 and E2, be two ellipses whose centers are at the origin.The major axes of E1 and E2, lie along the x-axis and the y-axis, respectively. Let S be the circle x2+(y−1)2=2. The straight line x+ y =3 touches the curves S, E1 and E2 at P,Q and R, respectively. Suppose that PQ=PR=2√23.If e1 and e2 are the eccentricities of E1 and E2, respectively, then the correct expression(s) is(are):
View SolutionLet the equation of a curve passing through the point (0,1) be given b y=∫x2ex3dx. If the equation of the curve is written in the form x=f(y), then f(y) is
View SolutionLet E1 and E2, be two ellipses whose centers are at the origin.The major axes of E1 and E2, lie along the x-axis and the y-axis, respectively. Let S be the circle x2+(y−1)2=2. The straight line x+ y =3 touches the curves S, E1 and E2 at P,Q and R, respectively. Suppose that PQ=PR=2√23.If e1 and e2 are the eccentricities of E1 and E2, respectively, then the correct expression(s) is(are):
View SolutionLet E1 and E2, be two ellipses whose centers are at the origin.The major axes of E1 and E2, lie along the x-axis and the y-axis, respectively. Let S be the circle x2+(y−1)2=2. The straight line x+ y =3 touches the curves S, E1 and E2 at P,Q and R, respectively. Suppose that PQ=PR=2√23.If e1 and e2 are the eccentricities of E1 and E2, respectively, then the correct expression(s) is(are):
View SolutionLet E1andE2 be two ellipse whsoe centers are at the origin. The major axes of E1andE2 lie along the x-axis , and the y-axis, respectively. Let S be the circle x2+(y−1)2=2 . The straigth line x+y=3 touches the curves, S, E1andE2 at P,Q and R, respectively . Suppose that PQ=PR=2√23. If e1ande2 are the eccentricities of E1andE2 respectively, thent hecorrect expression (s) is (are)
View Solution
