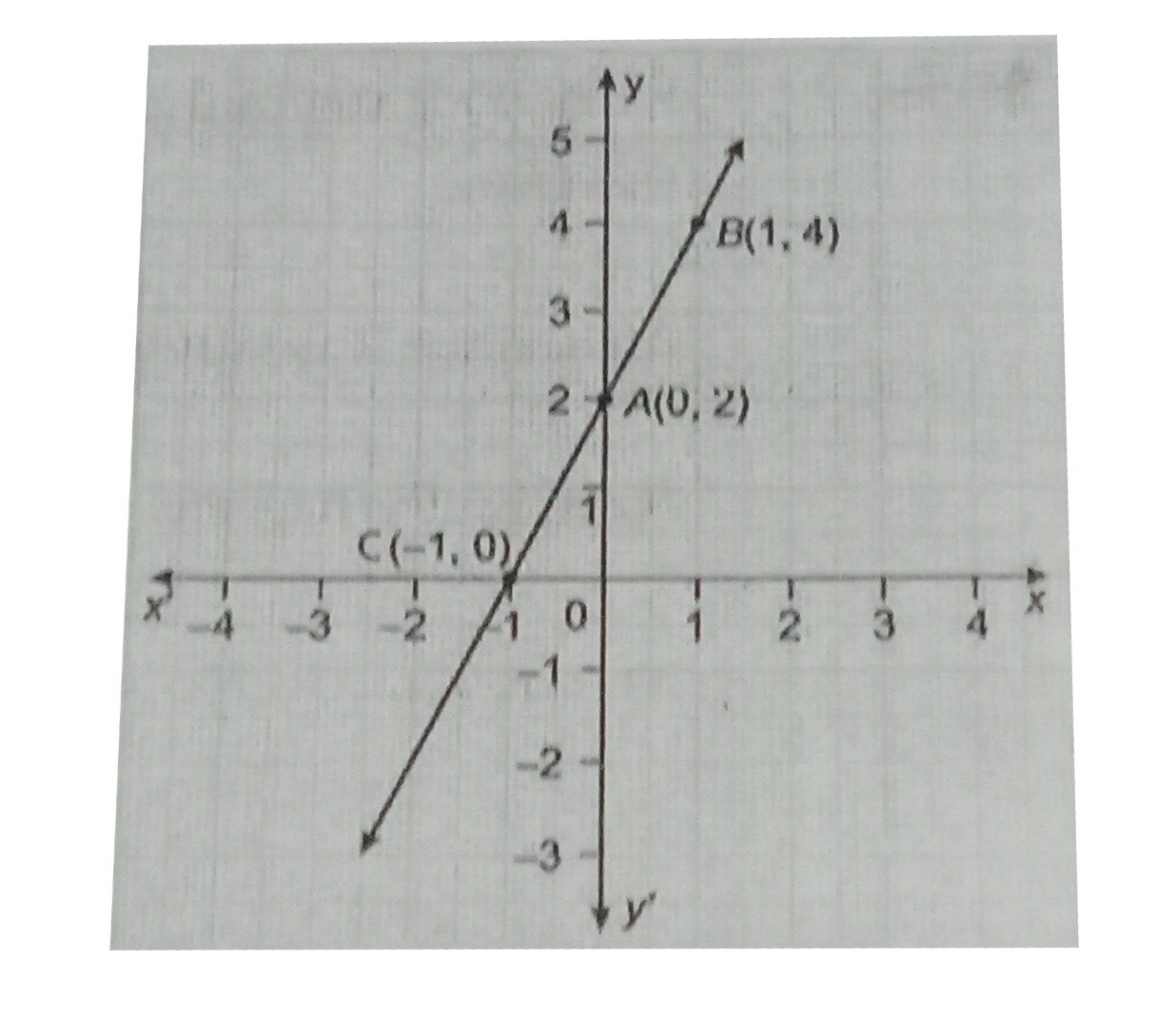
Plot the points A(0,2),B(1,4) and C(−1,0) on a graph paper and check whether they are collinear (lie on the same straight line) or not.
Video Solution
Text Solution
Plot the points A(0,2),B(1,4) and C(−1,0) on the graph paper as usual. On joining the points A and B by a straight line, we find that the points C(−1,0) lies on this line. Hence, the given points A(0,2),B(1,4) and C(−1,0) are collinear.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Problems From NCERT/ Exemplar6videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Revision Exercise8videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - EXAMPLE SOLUTION.19videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the points A(1,2) , B(0,0) and C (a,b) are collinear , then
Aa=bBa=2bC2a=bDa=-b - Question 2 - Select One
If the points (a, 0), (0, b) and (1, 1) are collinear, then
A1a2+1b2=1B1a2−1b2=1C1a+1b=1D1a−1b=1
The points A(-2,1), B(0,5) and C(-1,2) are collinear.
View SolutionPlot the points (4, 4), (1, 3), (4, 2) and (7, 3) on a graph paper and connect them with line segments. Name the shape formed by these points.
View SolutionAre the points A(0,2),B(1,−0.5),C(2,−3) collinear ?
View SolutionPlot the point A(2,5),B(−2,2)andC(4,2) on a graph paper. Join AB, BC and AC. Calculate the area of △ABC.
View SolutionIn a __________ graph, all the points on the graph lie on the same straight line.
View SolutionPlot the points (3,5)and(−1,3) on a graph paper and verify that the straight line passing through these points also passes through the point (1,4)
View Solution

