Point P (h,k) divides a line segment between the exes in the ratio $1 : 2$ Find the lengths (intercepts) on the axes made by this segment. Also find the area of triangle formed by the line segment and the axes.

Text Solution

Verified by Experts

Let AB be the line segment joining A (0.y) and B (x,0) between the axes.
P (h,k) divides the line segment in the ratio $1 : 2 .$
Now, question arises that whether $P A : P B = 1 : 2$ or $P B : P A = 1 : 2$ or $P B : P A = 1 : 2$
The answer of this is that always we take the former part of ratio towards the X-axis and latter part of ratio towards the Y-axis.

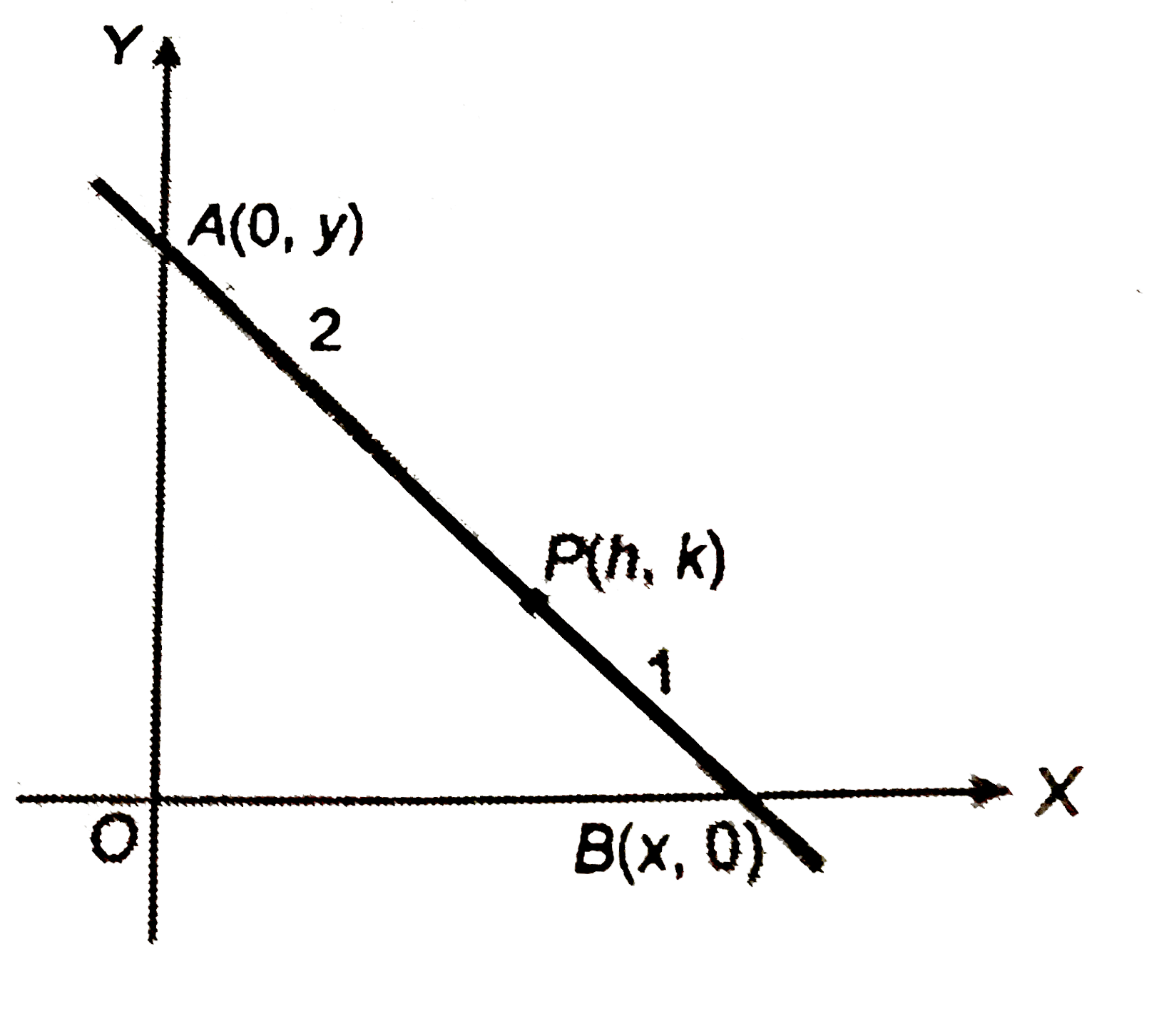
So, here we will take
$P B, P A = 1 : 2$
$∴$ By using section formula,
$h = \frac{1 (0) + 2 (x)}{1 + 2} \Rightarrow h = \frac{2 x}{3} \Rightarrow x = \frac{3 h}{2}$
and $k = \frac{1 (y) + 2 (0)}{1 + 2} \Rightarrow k = \frac{y}{3} \Rightarrow y = 3 k$
So, length of intercept on the X-axis $= O B = x = \frac{3 h}{2}$
and the length of intercept on the Y-axis =OA = y = 3k.
$∴$ Area of $Δ A O B = \frac{1}{2} \times O B \times O A = \frac{1}{2} \frac{3 h}{2} \times 3 k = \frac{9}{4} h k$ square units

Updated on:21/07/2023

A point R (h, k) divides a line segment between the axis in the ratio 1 : 2 what will be the equation on line
A $\frac{x}{h} - \frac{2 y}{k} = 4$
B $\frac{x}{h} + \frac{2 y}{k} = 3$
C $\frac{x}{k} + \frac{y}{h} = 1$
D $\frac{x}{2 k} + \frac{y}{h} = 1$
If (-5,4) divides the line segment between the coordinate axes in the ratio $1 : 2$ then what is its equation ?
A8x + 5y + 20 = 0
B5x + 8y -7 = 0
C8x - 5y + 60 = 0
D5x -8y + 57 = 0
If (-5, 4) divides the line segment between the coordinate axes in the ratio 1: 2, then what is its equation?
A8 x + 5y + 20 = 0
B5x +8y - 7 = 0
C8x - 5y + 60 = 0
D5x - 8y + 57 = 0