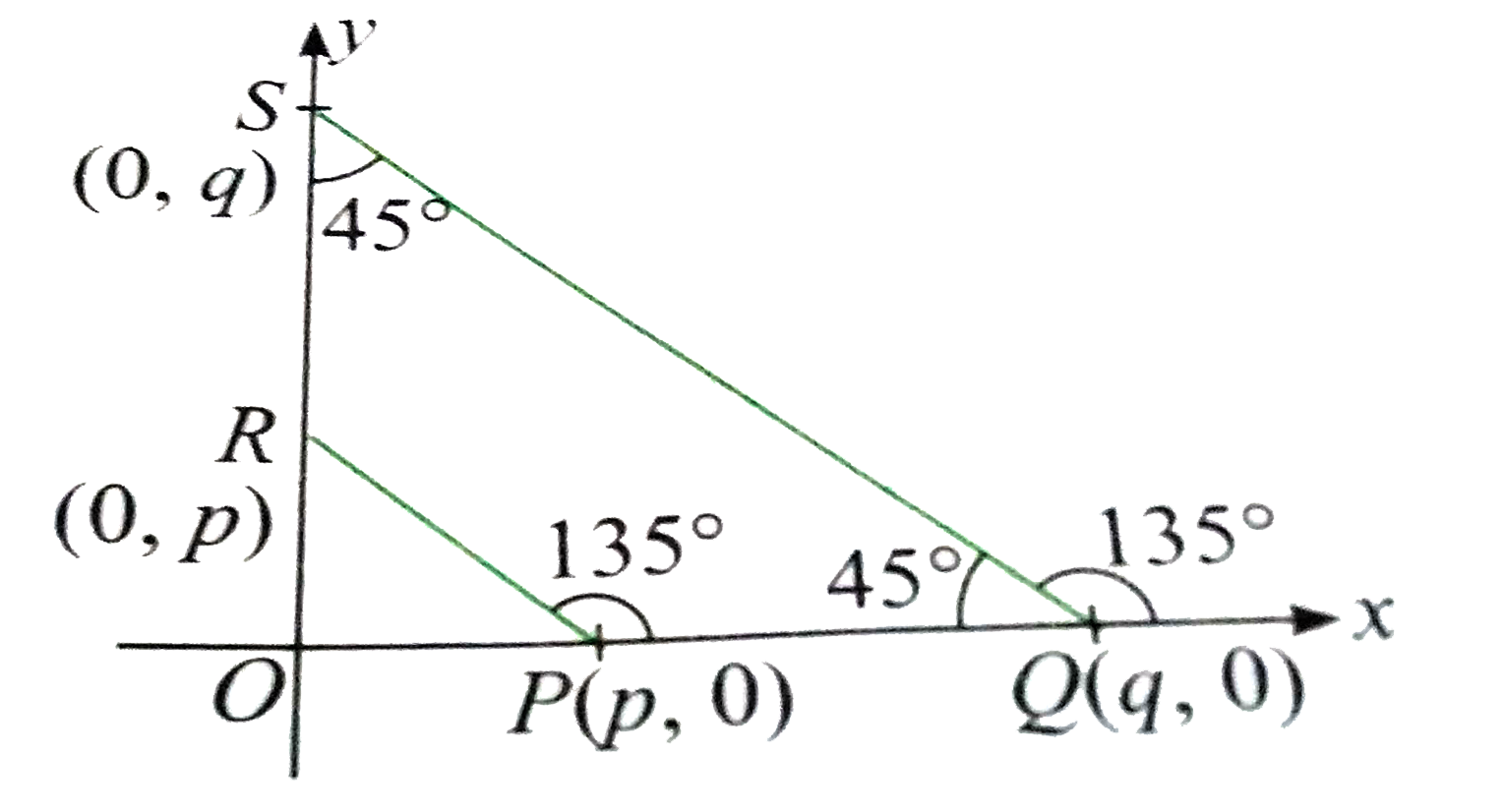
Point P(p,0),Q(q,0),R(0,p),S(0,q) from.
parallelogram
rhombus
cyclic quadrilateral
none of these
The correct Answer is:C
The diagram is self -explanatory. From the diagram, PQRS is a cyclic quadrilateral.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked10videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.69videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Point P(p,0),Q(q,0),R(0,p),S(0,q) form (a) parallelogram (b) rhombus (c) cyclic quadrilateral (d) none of these
View SolutionConsider the points P(p,0,0),Q(0,q,0)andR(0,0,r) where pqr≠0 then the equation of the plane PQR is (A) px+qy+r=1 (B) xp+yq+zr=1 (C) x+y+z+1p+1q+1r=0 (D) none of these
View SolutionPlot the following points on the graph paper : P(3,0) (ii) Q(−4,0) R(0,5) (iv) S(0,−7) (fig)
View SolutionPlot the following points on the graph paper : P(3,0) (ii) Q(−4,0) R(0,5) (iv) S(0,−7) (fig)
View SolutionThe points (p,q +r) , (q, r+p) and (r, q+p) are _______.
View SolutionIf P=⎡⎢⎣x000y000z⎤⎥⎦ and Q=⎡⎢⎣a000b000c⎤⎥⎦ , prove that PQ=⎡⎢⎣xa000yb000zc⎤⎥⎦=QP
View SolutionFind the vector joining the points P(2,3,0)and Q(1,2,4)directed from P to Q.
View SolutionIf P(0, 1, 2), Q(4, -2, 1) and R(0, 0, 0) are three
points, then ∠PRQ isView SolutionIf the point (0,0),(2,2√3), and (p,q) are the vertices of an equilateral triangle, then (p ,q) is
View SolutionFour charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
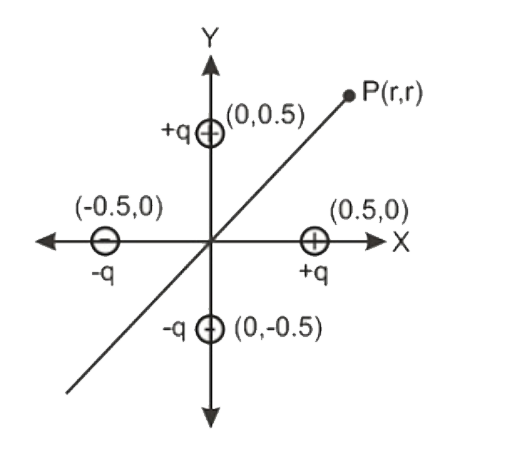
The electric field due to these charges at a point P(r,r), where r>>0.5, will beView Solution
