Point P(x, y) is rotated by an angle $θ$ in anticlockwise direction. The new position of point P is $Q (x_{1}, y_{1})$ . If $[\begin{matrix} x_{1} y_{1} \end{matrix}] = A [\begin{matrix} x y \end{matrix}]$ , then find matrix A.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $A = [\begin{matrix} cos θ & - sin θ sin θ & cos θ \end{matrix}]$

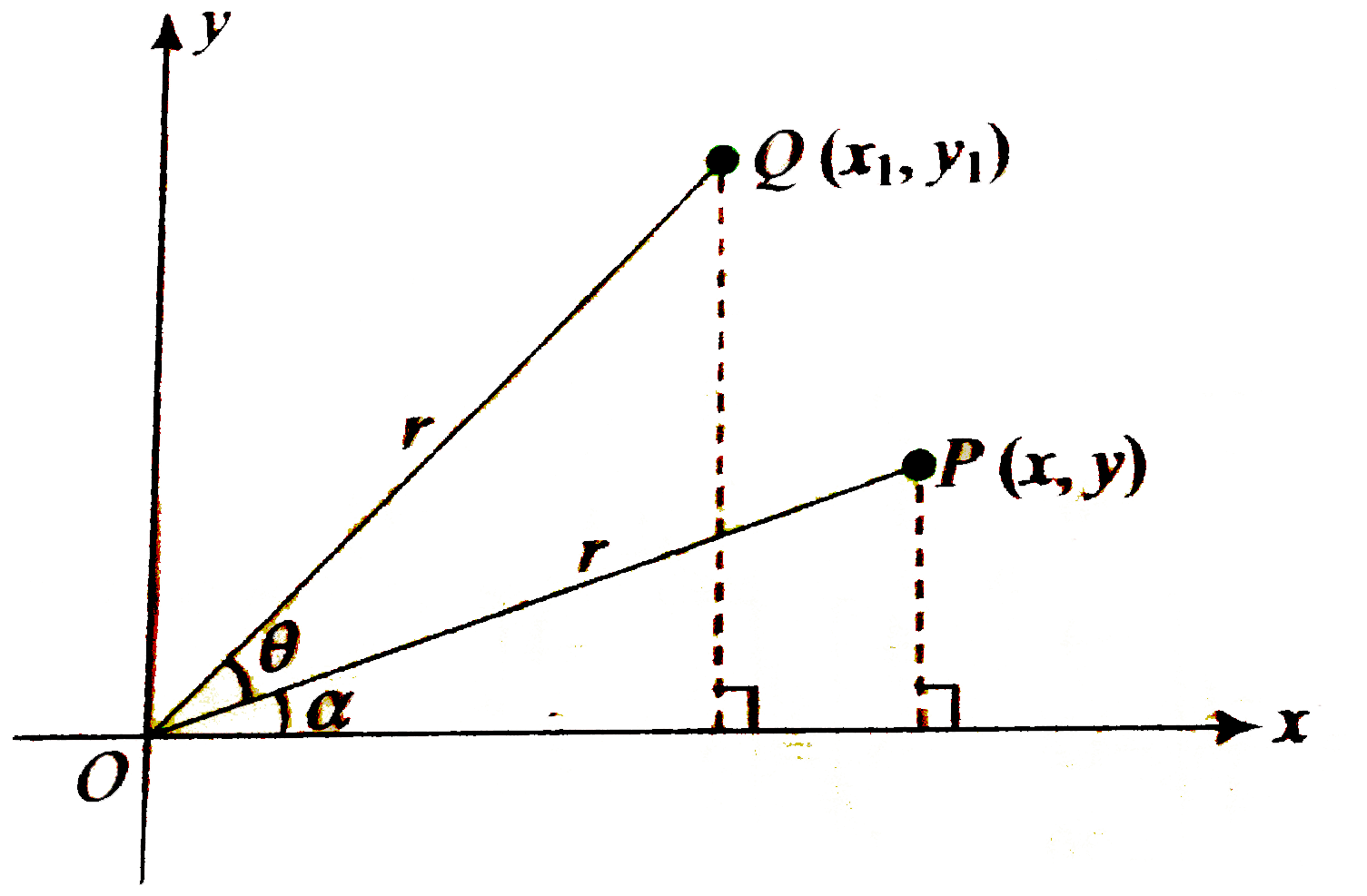
From the figure, $x_{1} = r cos (θ + α)$
$= (r cos α) cos θ - (r sin α) sin θ$
$∴ X_{1} = x cos θ - y sin θ$
and $y_{1} = r sin (θ + α) = (r sin α) cos θ + (r cos α) sin θ$
$∴ Y_{1} = x sin θ + y cos θ$
So, $[\begin{matrix} x_{1} y_{1} \end{matrix}] = [\begin{matrix} cos θ & - sin θ sin θ & cos θ \end{matrix}] [\begin{matrix} x y \end{matrix}]$
$∴ A = [\begin{matrix} cos θ & - sin θ sin θ & cos θ \end{matrix}]$

|

Updated on:21/07/2023

Class 12 MATHS MATRICES

Topper's Solved these Questions

Similar Questions

CENGAGE-MATRICES-Exercise 13.4

Home
Ask Doubt
Profile