PQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
Let the height of the tower PQ be h.
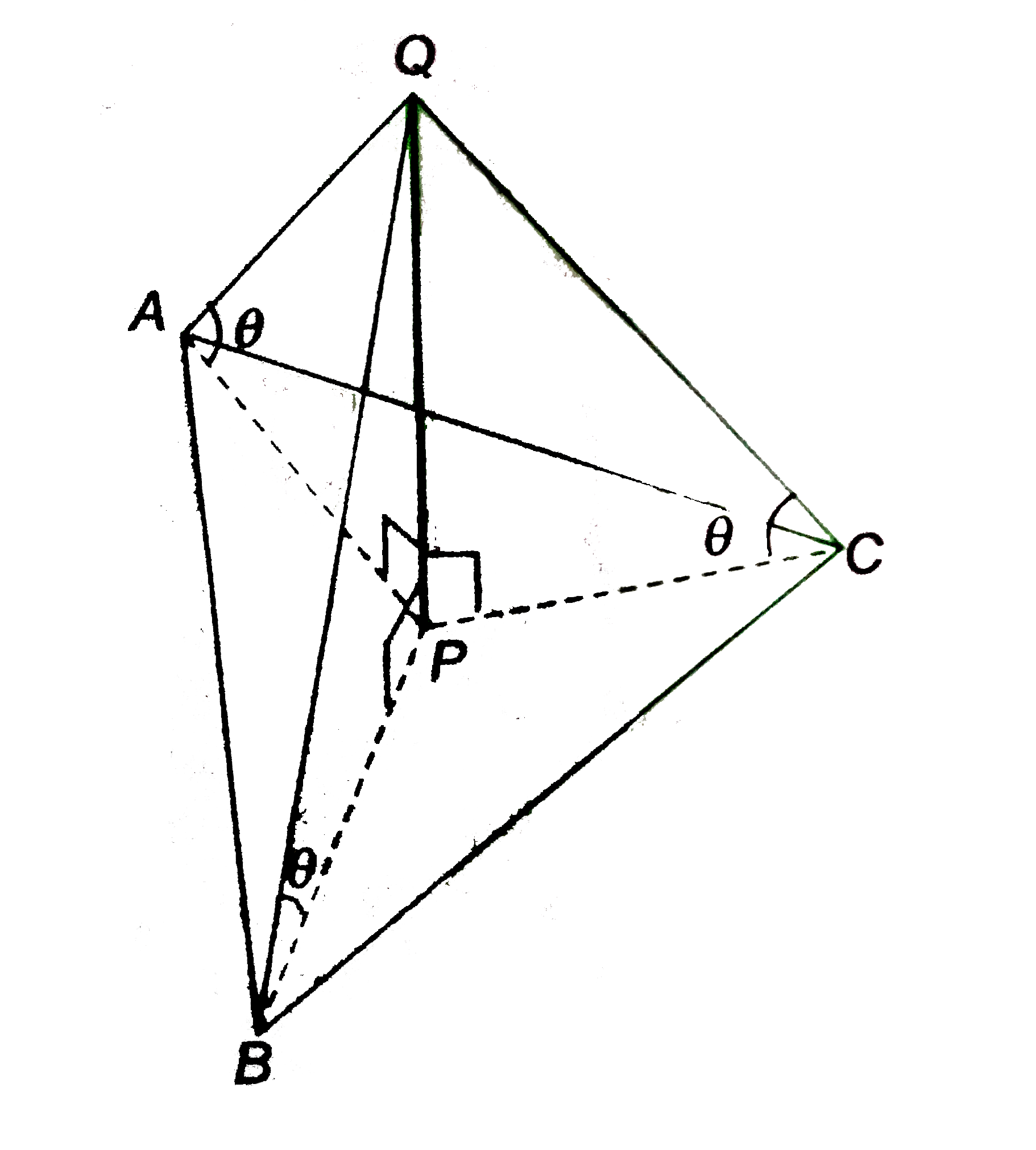
AP = BP =CP =hcotθ
Therefore , P is the circumcentre of ΔABC
∴AP=BP=CP=R=abc4Δ
∴h=abc4Δtanθ
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - Exercise18videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year14videos
HYPERBOLA
Similar Questions
PQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
View SolutionThe vertices of triangle ABC are A (4, 4), B (6, 3), C (2, -1), then angle ABC is equal to
View Solution
Knowledge Check
- Question 1 - Select One
PQ is a vertical tower and A, B, C are three points on a horizontal line through Q, the foot of the tower and on the same side of the tower. If the angles of elevation of the top of the tower from A, B and C are α,β,γ respectively, then AB/BC =
Acotα−cotγcotβ−cotγBcotα−cotβcotβ−cotγCcotα−cotβcotα−cotγDcotα−cotγcotα−cotβ - Question 2 - Select One
A vertical tower CP subtends the same angle θ, at point B on the horizontal plane through C, the foot of the tower, and at point A in the vertical plane. If the triangle ABC is equilateral with length of each side equal to 4 m, the height of the tower is
A8√3 mB4√3/3 mC4√3 mD8/√3 m - Question 3 - Select One
The angle of elevation of the top Q of a tower PQ at a point A on the horizontal plane through P the foot of the tower is α. At a point B on AQ at a vertical height of a, the angle of elevation of the middle point R of the tower PQ is β, then the height of the tower is
A2a(tanα−tanβ)tanα−2tanβB2a(tanα−2tanβ)tanα−tanβC2(tanαtanβ−1)2tanαcotβ−1D2a(tanαcotβ−1)2tanαcotβ−1
ABC is a vertical tower such that AB=BC=x from the foot A of the tower a horizontal line AQP is drawn.If the angle of elevation of the point B from P is α and that of C from Q is 2α then (AP)(PQ) is equal to
View SolutionThe angle of elevation of the top of the tower observed from each of three points A,B , C on the ground, forming a triangle is the same angle α. If R is the circum-radius of the triangle ABC, then find the height of the tower
View SolutionSides of triangle ABC are in A.P. if a<min{b,c} then cosA is equal to
View SolutionIf a,b,c are sides of ΔABC are in A.P. then
View SolutionAngle A, B, C of a triangle ABC are equal to each other. Prove that ABC is equilateral.
View Solution

