PQRS is a rhombus with ∠PQR=54∘. Determine ∠PRS.
The correct Answer is:⇒ ∠PRS=63∘
To solve the problem of finding angle PRS in rhombus PQRS where angle PQR = 54°, we can follow these steps:
1. Understanding the Rhombus Properties:
A rhombus has opposite angles that are equal and its diagonals bisect each other at right angles (90°).
2. Identify Given Information:
We know that angle PQR = 54°.
3. Determine Angle QRS:
Since opposite angles in a rhombus are equal, angle PSQ (which is opposite to angle PQR) is also 54°.
4. Calculate Angle QRP:
The diagonals bisect the angles. Therefore, angle QRP is half of angle PQR:
Angle QRP=54°2=27°
5. Identify Triangle SOR:
Consider triangle SOR formed by the diagonals. Since the diagonals intersect at right angles, angle SOR = 90°.
6. Use the Triangle Angle Sum Property:
The sum of angles in triangle SOR is 180°:
Angle SOR+Angle QRP+Angle PRS=180°
Substituting the known values:
90°+27°+Angle PRS=180°
7. Solve for Angle PRS:
117°+Angle PRS=180°
Angle PRS=180°−117°=63°
Final Answer:
Angle PRS = 63°.
A rhombus has opposite angles that are equal and its diagonals bisect each other at right angles (90°).
We know that angle PQR = 54°.
Since opposite angles in a rhombus are equal, angle PSQ (which is opposite to angle PQR) is also 54°.
The diagonals bisect the angles. Therefore, angle QRP is half of angle PQR:
Angle QRP=54°2=27°
Consider triangle SOR formed by the diagonals. Since the diagonals intersect at right angles, angle SOR = 90°.
The sum of angles in triangle SOR is 180°:
Angle SOR+Angle QRP+Angle PRS=180°
Substituting the known values:
90°+27°+Angle PRS=180°
117°+Angle PRS=180°
Angle PRS=180°−117°=63°
Angle PRS = 63°.
Topper's Solved these Questions
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - QUESTION BANK - 23
20 Videos
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - SELF ASSESSMENT SHEET - 23
10 Videos
- PERCENTAGE AND ITS APPLICATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )
10 Videos
- PROBABILITYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - SELF ASSESSMENT SHEET -29
10 Videos
Similar Questions
Knowledge Check
PQRS is a rhombus in which ∠R = 60°. Then PR : QS =
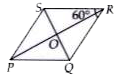 A√3 : 1B√3:√2C3 : 1D3 : 1
A√3 : 1B√3:√2C3 : 1D3 : 1PQRS is a rhombus in which ∠SPQ=64∘. Equilateral triangles PXQ and QYR are drawn outside the rhombus on sides PQ and QR. Calculate the magnitude of the angle ∠QXY.
A26∘B28∘C30∘D45∘If PQRS is a rhombus and ∠SPQ=50∘, then ∠RSQ is
A55∘B65∘C75∘D45∘
□ PQRS is a rhombus and ∠PQS=42∘ , then find ∠ PQR. Justify .
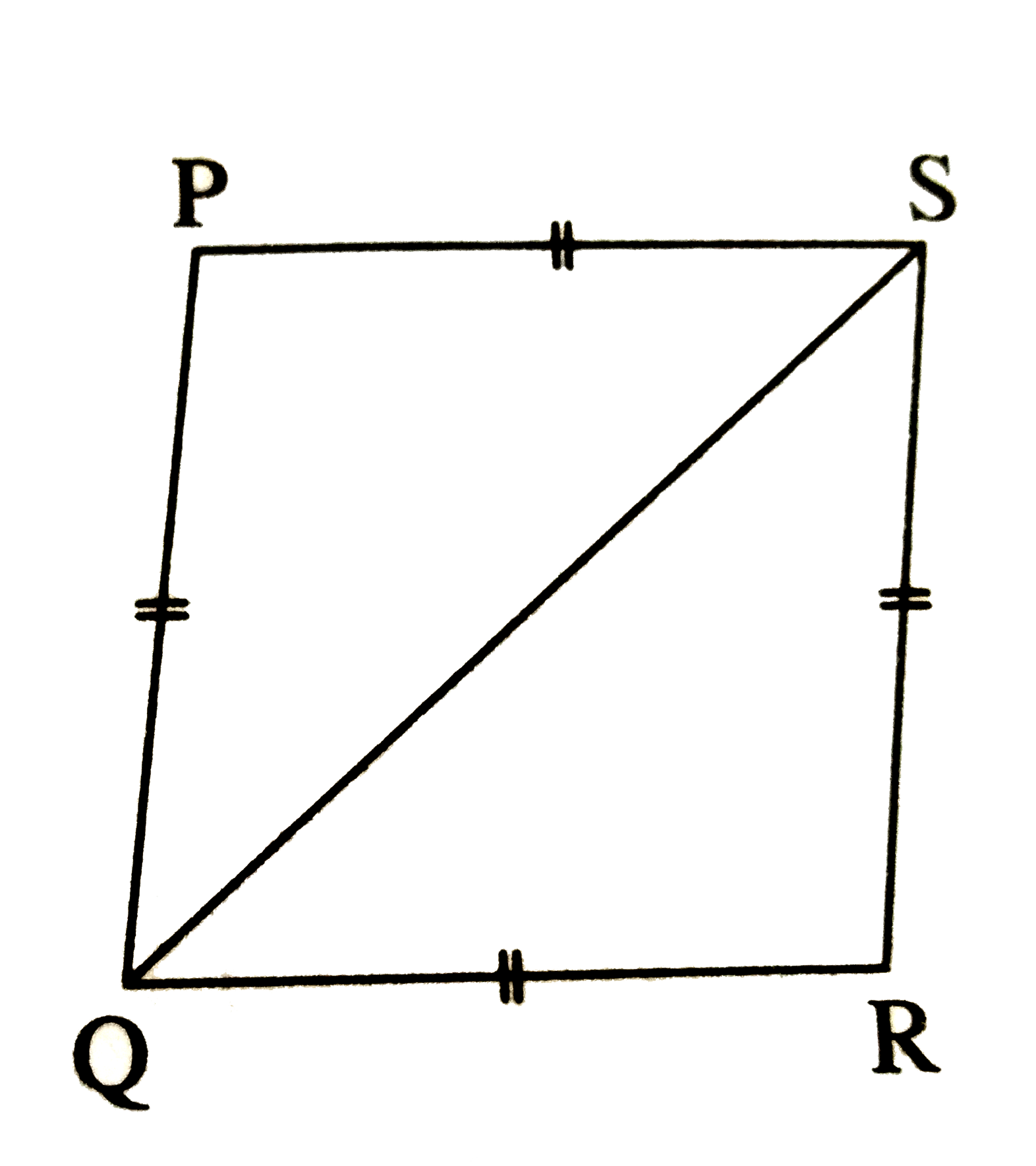
View Solution
In the figure above, PQRS is a square , ∠PTR=110∘, then find ∠TPS.
View SolutionPQRS is parallelogram. ∠Q is 70∘, then find ∠S.
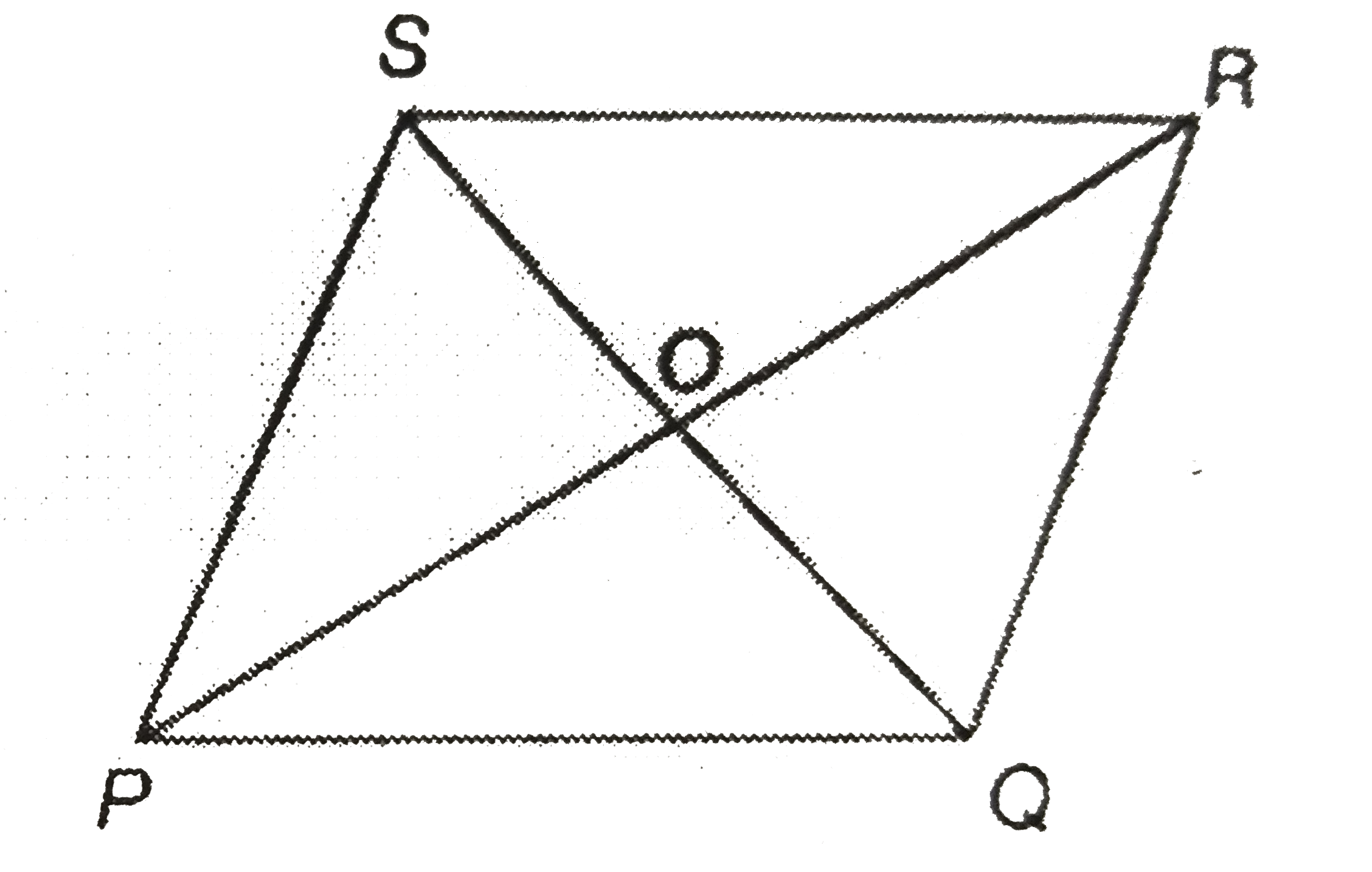
View SolutionIn the following, PQRS is a rhombus, SQ and PR are the diagonals of the rhombus intersecting at O. If angle OPQ=35∘, then find the value of angle ORS + angle OQP.
View SolutionIn △ PQR, PQ = PR, QR is extended to S and ∠PRS=110∘. Then, ∠PQR = .........
View Solution
