Question

Prove Equal chords of a circle subtend equal angles at the centre.

Explanation

This theorem states that, if there are 2 equal chords in a circle, the angles formed by the equal chords at the center of the circle are equal.



Given


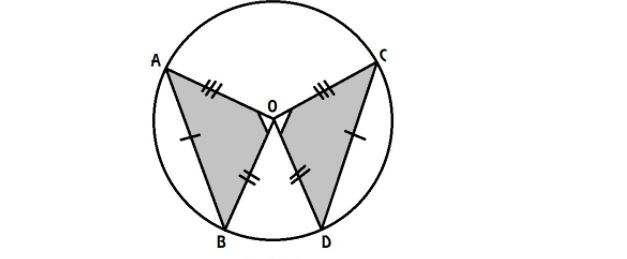
AB and CD are two equal chords in a circle with center O.



To Prove


`∠AOB = ∠COD`




Proof


Consider` ΔAOB` and `ΔCOD`


`AO = OC` [radii of the same circle]


`BO = OD` [radii of the same circle]


`AB = CD` [Given]


∴ `ΔAOB ≅ ΔCOD` by SSS congruency.


`∠AOB = ∠COD` [CPCT]



Hence Proved.