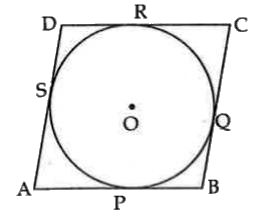
Prove that a parallelogram circumscribing by a circle is always a rhombus. Solution in Bengali
Let ABCD is a parallelogram circumscribing by a circle with centre at O.
We have to prove that ABCD is a rhombus.
Proof: Let the circle touches the parallelogram ABCD at the points P, Q, R and S.
Then AP and AS are two tangents to the circle from the extenrnal point A.
∴AP=AS........(1)
Similarly, BP=BQ.........(2)
CQ=CR...........(3)and
DR=DS.........(4)
Now ∵ ABCD is a parallelogram,∴AB=DCandAD=BC.
Now, AB+DC=AP+BP+DR+CR
=AS+BQ+DS+CQ
=AS+DS+BQ+CQ
=AD+BC
or, AB+AB=BC+BC[∵DC=ABandAD=BC]
or,2AB=2BCor,AB=BC
Similarly, AD=DC,∴AB=BC=CD=DA
∴ four sides of the parallelogram ABCD are equal ABCD is also a parallelogram
∴ABCD is a rhombus. (Provide)

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View SolutionIf a parallelogram circumscribes a circle then prove that it must be a rhombus.

View Solutionसिद्ध कीजिए किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
View SolutionProve that the parallelogram circumscribed about a circle is only a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View Solution
