
Prove that, angles inscribed in the same arc are congruent .
Given : ∠PQRand∠PSR are inscribed in the same arc PXR. PXR is intercepted by the angles.
To prove : ∠PQR≅∠PSR
Proof :
m∠PQR=12m(arcPXR) (I)
□
m∠.........=12m(arcPXR) (II)
∴m∠.......=m∠PSR (From I and II)
∴∠PQR≅∠PSR ( Angles equal in measure are congruent )
Inscribed angle theorem , PSR, Inscribed angle theorem , PQR
Topper's Solved these Questions
Similar Questions
Prove that, angles inscribed in the same are arc congruent.
 View Solution
View SolutionProve that, angles inscribed in the same arc are congruent
∠PQR and ∠PSR are inscribed in the same arc.
Arc PXR is intercepted by the angles.
To prove :∠PQR≅∠PSR

Proof :
m∠PQR=12m(arcPXR) …...□
m∠□=12m(arcPXR) ....(2) □
∴m∠□=m∠PSR ......[ From (1) and (2) ]
∴∠PQR≅∠PSR ...(Angles equal in measure are congrument )View Solution
Knowledge Check
- Question 1 - Select One
In △PQR , if ∠R>∠Q then
AQR>PRBPQ>PRCPQ<PRDQR<PR - Question 2 - Select One
I is the incentre of a triangle PQR and ∠=107∘ then find the value ∠P.
A56°B34°C26°D42° - Question 3 - Select One
A triangle ABC is inscribed in a circle and the bisectors of the angles A, B and C meet the cir cumference at P, Q and R respec tively. The angles of the triangle PQR respectively are
A90∘−A2,90∘+A290∘+C2B90∘+A2,90∘−B2,90∘−CC90∘−A2,90∘−B2,90∘−C2DNone of these
Prove that an angle inscribed in a semi-circle is a right angle using vector method.
View SolutionIn the figure, ∠PQR and ∠PSR are inscribed in the same are PQR and they intercept same are PR. If ∠PQR=65∘ then find the measure of ∠PSR
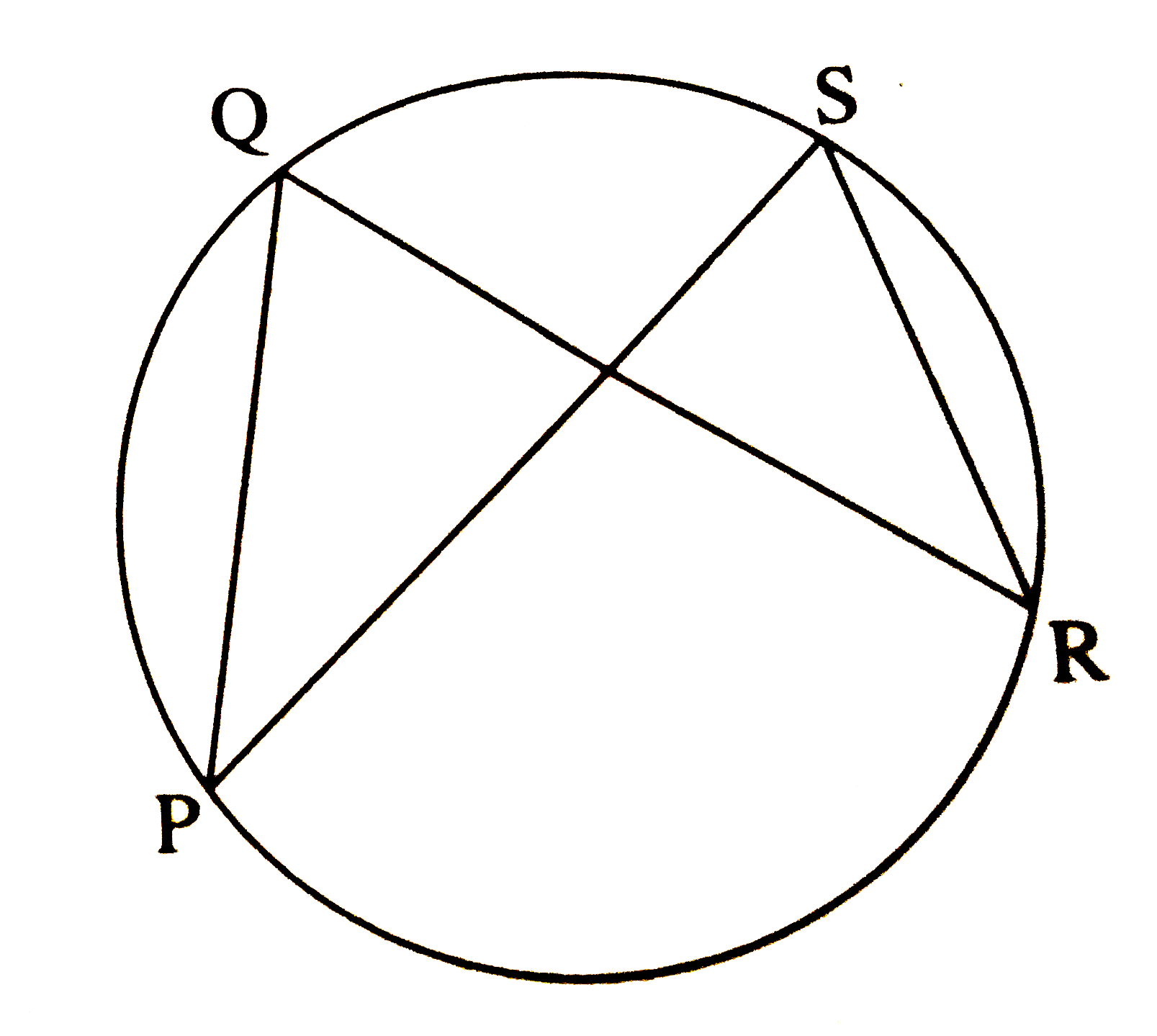 View Solution
View SolutionIn Fig. 6.15, angle PQR= angle PRQ, then prove that angle PQS= angle PRT.
View SolutionCorollaries of inscribed angle theorem :
Angle inscribed in the same arc arc contruent
Given : (1) A circle with centre O
(2) ∠ABD and ∠ACD are inscribed in arc ABC and intercepts arc APD.
To prove : ∠ABD≅∠ACD
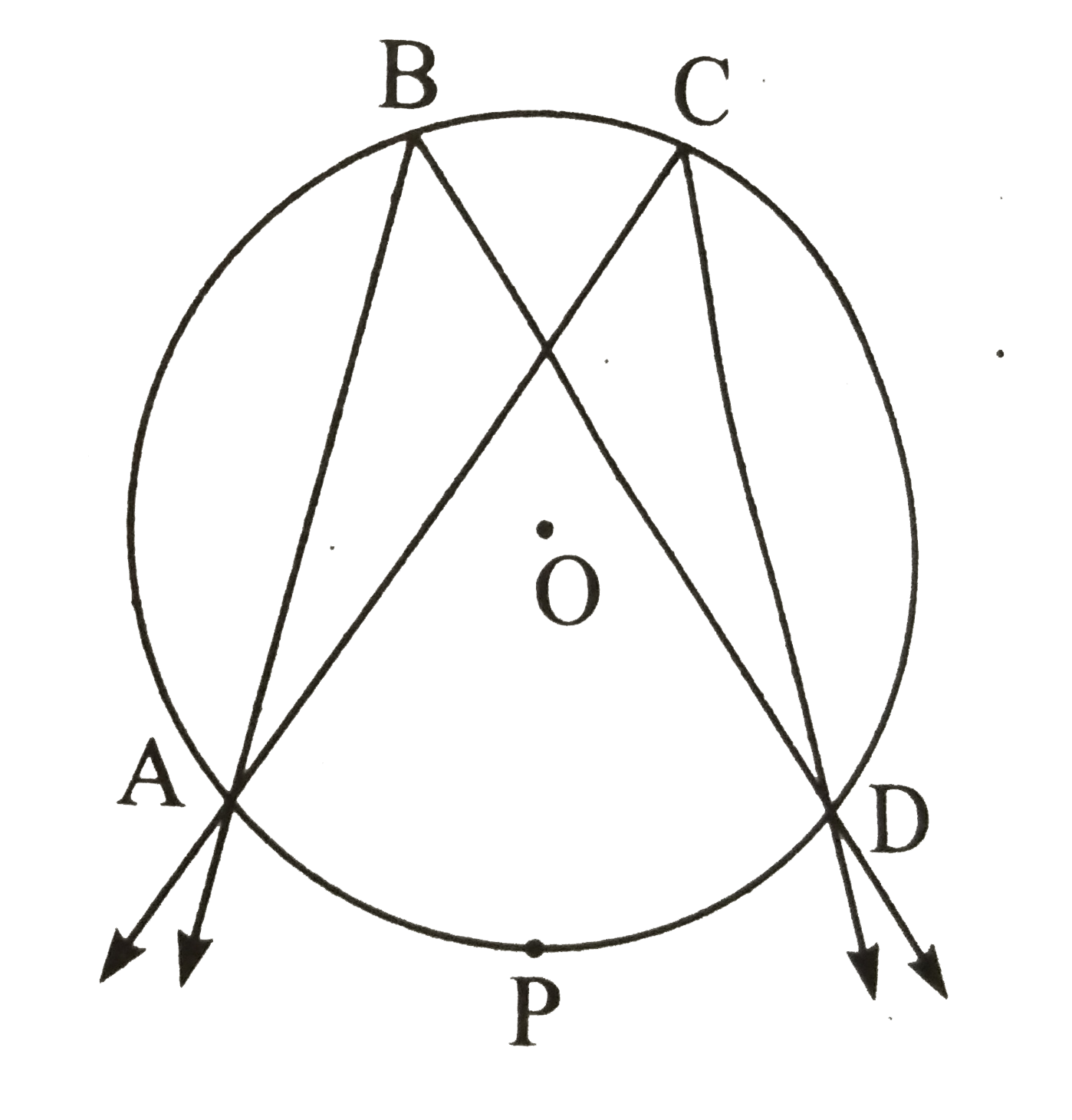 View Solution
View SolutionS is the incentre of △PQR . If ∠PSR=125∘, then the measure of ∠PQR is:
View Solution

