Prove that for x>−c, the minimum value of f(x) =(a+x)b+xc+x is 2√(c−a)(c−b) + a + b - 2c,given(c−a)(c−b)>0.Solution in Punjabi
Step by step video & image solution for Prove that for x> -c, the minimum value of f(x) =(a+x) (b+x)/(c+x) is 2sqrt((c-a)(c-b)) + a + b - 2c, given (c-a) (c-b) > 0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The length x of a rectangle is decreasign at the rate of 5 cm/min and the width y is incresaing at the rate of 4cm/min. when x = 8 cm and y = 6 cm, find the rates of change of the area of the rectangle.
View SolutionUsing integration, find the region bounded by the line 2y=-x+8, x-axis, and the lines x=2 and x=4.
View SolutionProve that the minimum value of (a+x)(b+x)(c+x)a,b>c,x≻c is (√a−c+√b−c)2
View SolutionProve that : ∣∣ ∣∣x+abcax+bcabx+c∣∣ ∣∣=x2(x+a+b+c)
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
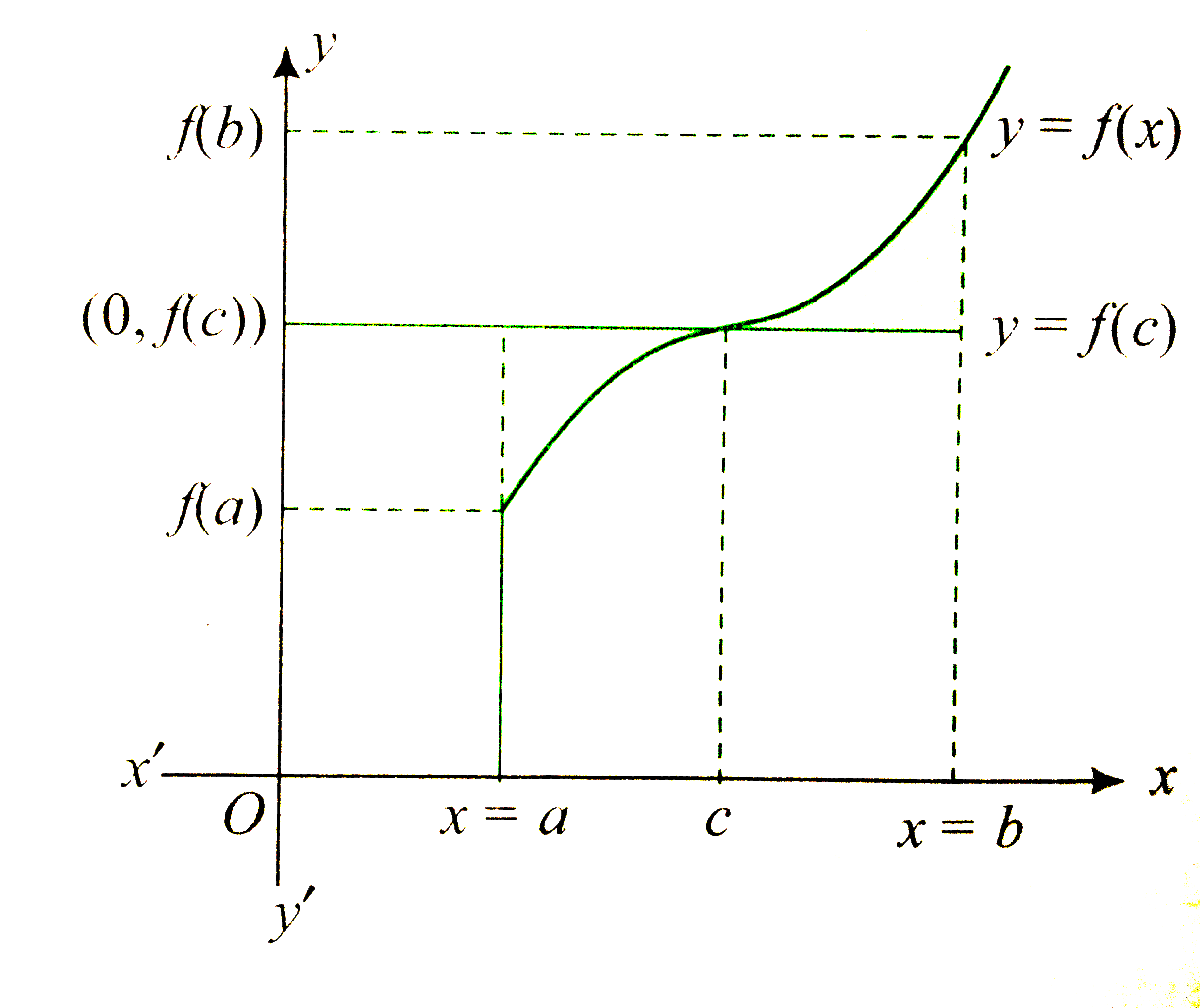
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View SolutionIf A=⎡⎢⎣a−b−c2a2a2bb−c−a2b2c2cc−a−b⎤⎥⎦
=(a+b+c)(x+a+b+c)2,x≠0 and a+b+c≠0, then x is equal to
View Solution(iii) सिद्ध करें की ∣∣ ∣∣x+abcax+bcabx+c∣∣ ∣∣=x2(x+a+b+c)
View SolutionIf F(x)=(x−b)(x−c)(a−b)(a−c)+(x−c)(x−a)(b−c)(b−a)+(x−a)(x−b)(c−a)(c−b), show that F(0)=1.
View Solutionयदि ∣∣ ∣∣a−b−c2a2a2bb−c−a2b2c2cc−a−b∣∣ ∣∣=(a+b+c)(x+a+b+c)2,x≠0 तथा a+b+c≠1, तो x बराबर है
View SolutionIf the roots of the equation x2+ax+b=0arecandd, then roots of the equation x2+(2c+a)x+c2+ac+b=0 are a c b. d−c c. 2c d. 0
View SolutionProve that the minimum value of (a+x)(b+x)(c+x)a,b>c,x≻c is (√a−c+√b−c)2
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View SolutionIf a+b+c=0and∣∣ ∣∣a−xcbcb−xabac−x∣∣ ∣∣=0 then find the value of x
View Solutionf(x)=(x−b)(x−c)(a−b)(a−c)+(x−c)(x−a)(b−c)(b−a)+(x−a)(x−b)(c−a)(c−b) হলে দেখাও যে, f(0)=1 ।
View SolutionProve that the minimum value of (a+x)(b+x)(c+x)a,b>c,x≻c is (√a−c+√b−c)2
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2) . "Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx =f(c)(c-a)-int_(a)^(c)(f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c) rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx Differentiating w.r.t. c, we get (dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0) For maxima and minima , (dA)/(dc)=0 rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0) Hence, c=(a+b)/(2) "Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0 Hence, A is minimum when c=(a+b)/(2) . If the area bounded by f(x)=(x^(3))/(3)-x^(2)+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View Solution