Prove that in an ellipse, the perpendicular from a focus upon any tangent and the line joining the centre of the ellipse to the point of contact meet on the corresponding directrix.
Video Solution
Text Solution
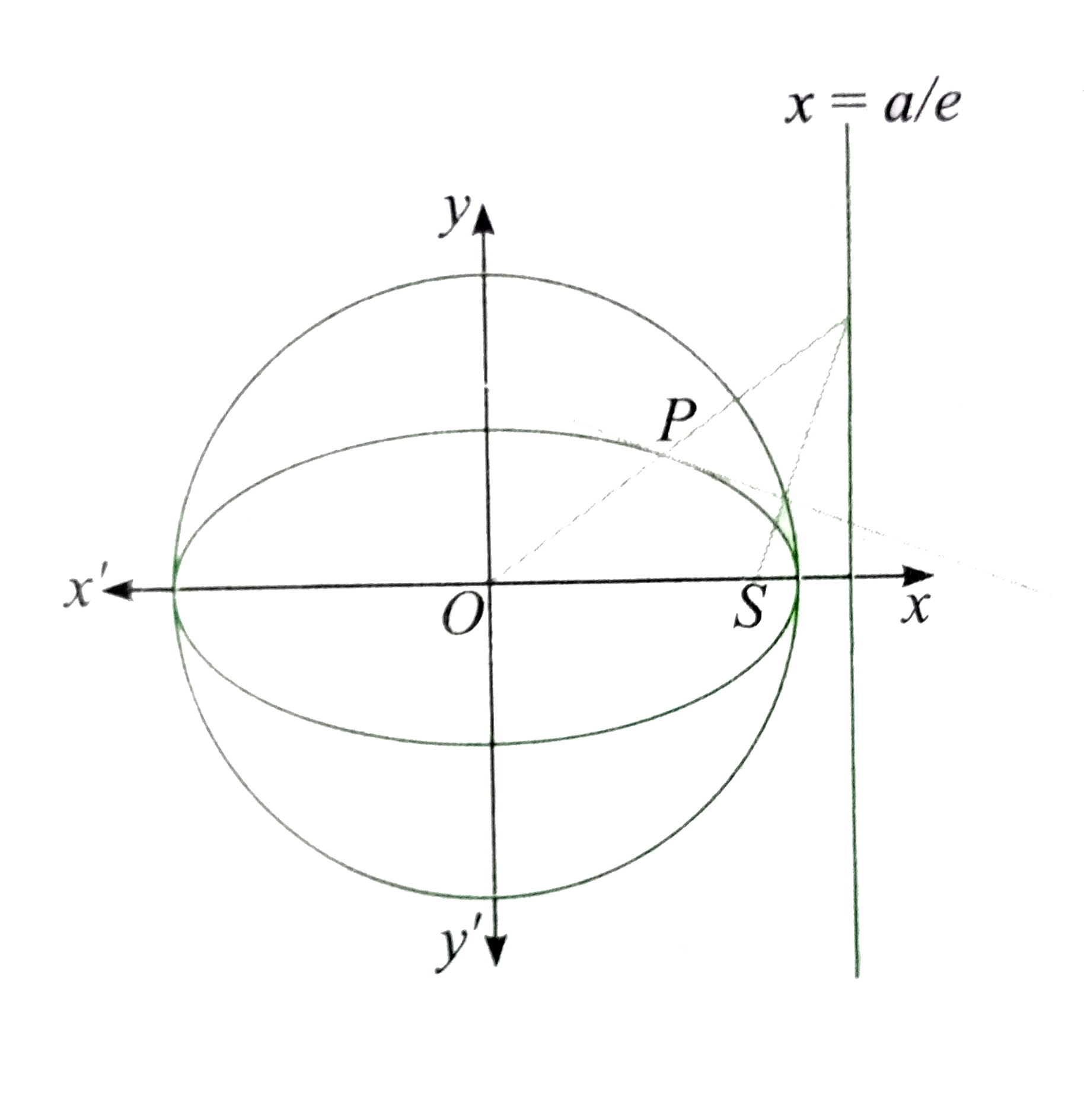
Let the elliopse be
x2a2+y2b2=1
and O be the center.
The tangent at P(x1,y1) is xx1a2+yy1b2−1=0
Whose slope is −b2x1/a2y1.
The focus of the ellipse is S (ae,o)
The equation of he line through S(ae,o) perpendicular to the tangent at P is
y=a2y1b2x2(a−ae) (1)
The equation of OP is
y=y1x1x (2)
Soving (1) and (2) , we get
x1y1x=a2y1b2x1(x−ae)
or x(a2−b2)=a3e
or xa2e2=a3e
orx=ae
This is the corresponding durectrix.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
The product of the perpendicular drawn from the foci upon any tangent to any ellipse
Adepends upon fociBis constantCdepends upon the tangentDnone of the above - Question 2 - Select One
The product of the perpendicular drawn from the foci upon any tangent to any ellipse
Adepends upon fociBis constantCdepends upon the tangentDnone of the above - Question 3 - Select One
The product of the perpendiculars drawn from the two foci of an ellipse to the tangent at any point of the ellipse is
Aa2Bb2C4a2D4b2
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionProduct of perpendiculars drawn from the foci upon any tangent to the ellipse 3x2+4y2=12 is
View SolutionThe product of the perpendiculars drawn from the two foci of an ellipse to the tangent at any point of the ellipse is
View SolutionThe locus of feet of perpendiculars from the focii upon any tangent is an auxilliary circle.
View SolutionLocus of foot of perpendicular from focus upon any tangent is tangent at vertex
View Solution

