Question

Prove that in an ellipse , the perpendicular from a focus upon any tangent and the line joining the centre of the ellipse of the point of contact meet on the corresponding directrix.

Explanation

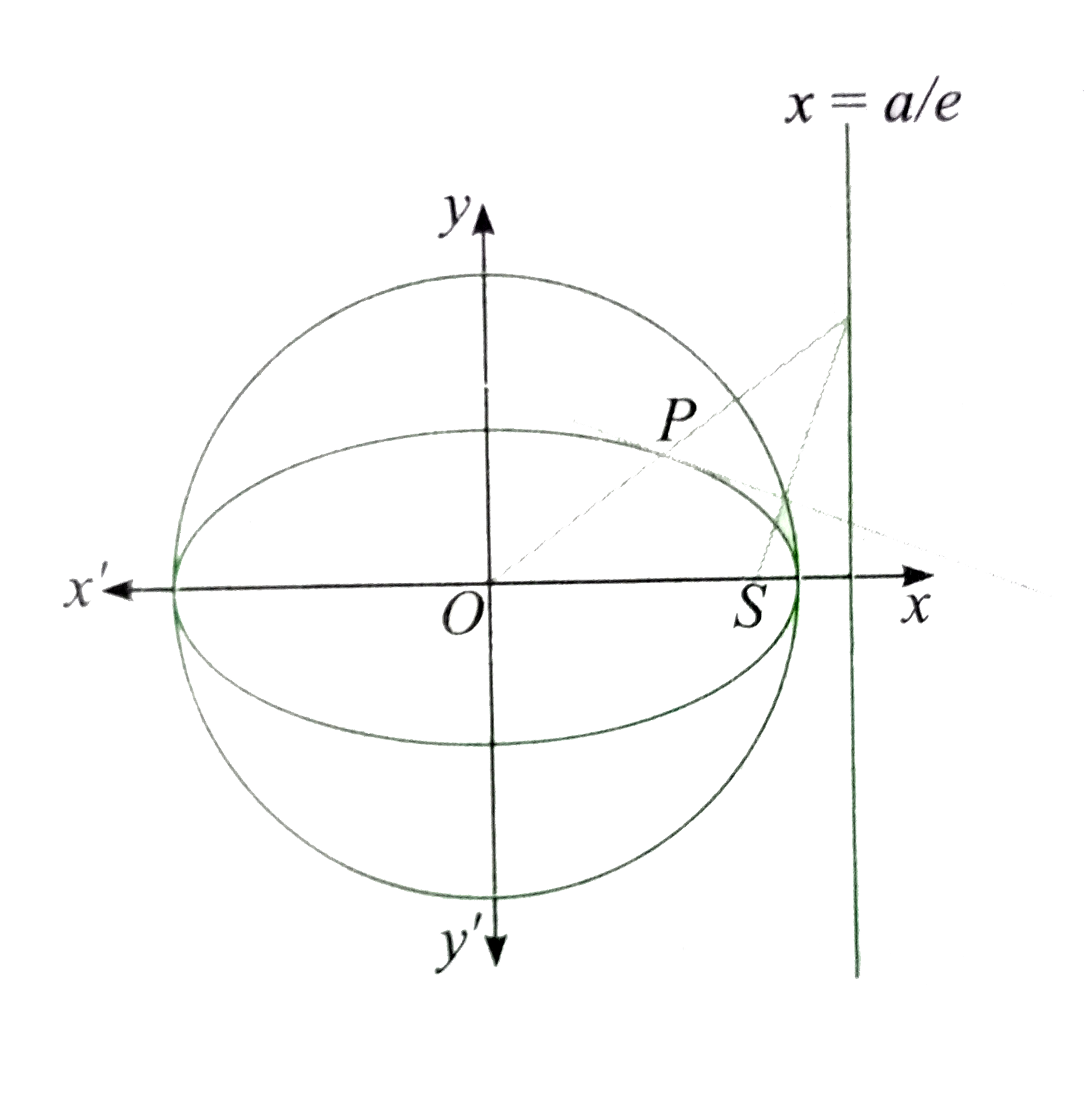
Let the elliopse be
`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
and O be the center.
The tangent at `P(x_(1),y_(1))` is `(x x_(1))/(a^(2))+(yy_(1))/(b^(2))-1=0`
Whose slope is `-b^(2)x_(1)//a^(2)y_(1)`.
The focus of the ellipse is S (ae,o)
The equation of he line through S(ae,o) perpendicular to the tangent at P is
`y=(a^(2)y_(1))/(b^(2)x^(2))(a-ae)" "(1)`
The equation of OP is
`y=(y_(1))/(x_(1))x" "(2)`
Soving (1) and (2) , we get
`(x_(1))/(y_(1))x=(a^(2)y_(1))/(b^(2)x_(1))(x-ae)`
or `x(a^(2)-b^(2))=a^(3)e`
or `xa^(2)e^(2)=a^(3)e`
`or x=(a)/(e)`
This is the corresponding durectrix.