Prove that the area of the parallelogram contained by the lines 4y−3x−a=0,3y−4x+a=0,4y−3x−3a=0, and 3y−4x+2a=0 is (27)a2.
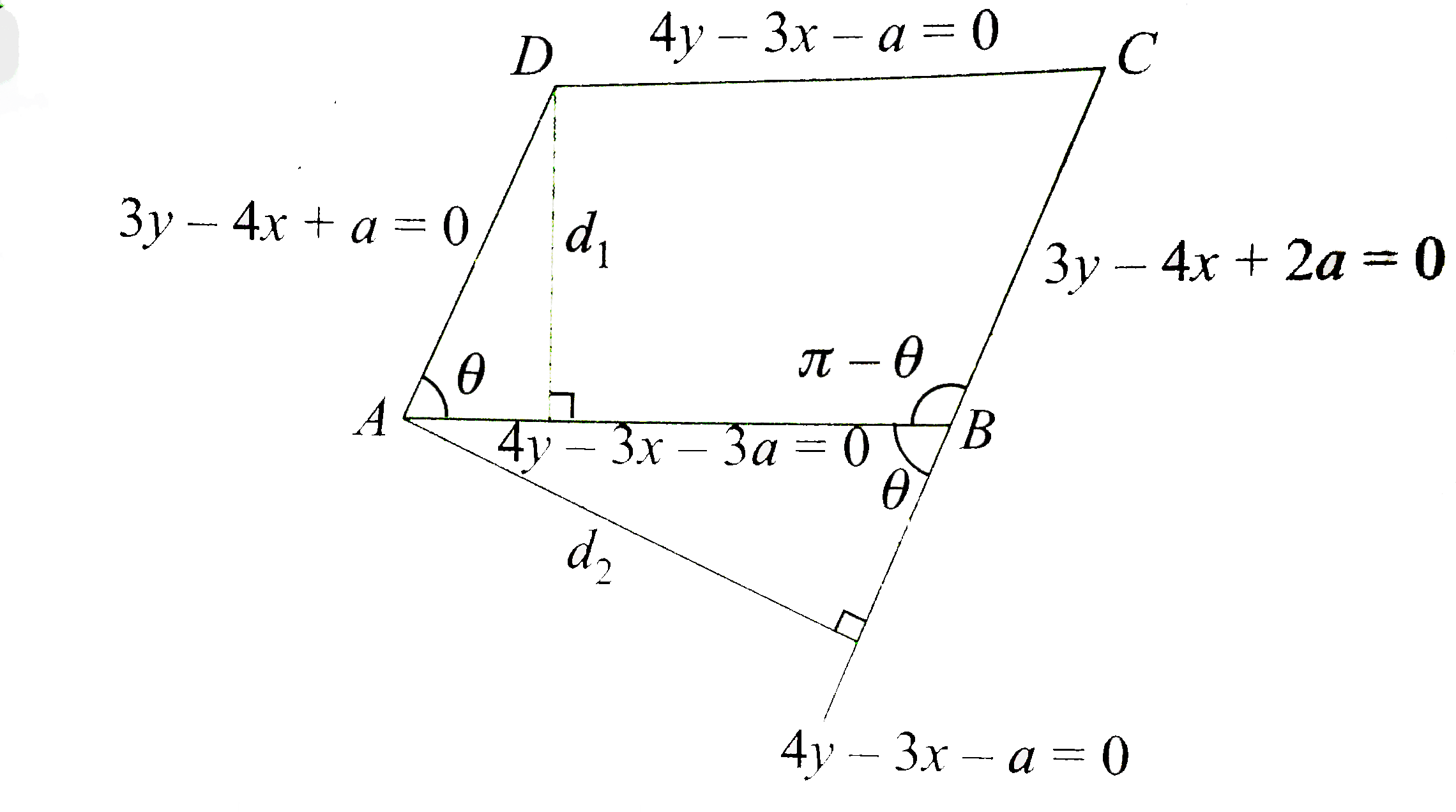
tanθ=∣∣∣(4/3)−(3/4)1+(4/3)×(3/4)∣∣∣=724
orcosecθ=257
Now d1=|−a+3a|5=∣2a5
and d2=|2a−a|5=∣∣∣a5∣∣∣
∴ Area=2(Area ofΔABD)=2(12d1⋅AB)
=d1d2cosec θ=(∣∣∣a5∣∣∣)(∣∣∣2a5∣∣∣)257=2a27
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE12videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Show that the area of the parallelogram formed by the lines 2x−3y+a=0, 3x−2y−a=0, 2x−3y+3a=0 and 3x−2y−2a=0 is2a25sq.units.
View SolutionThe area of the parallelogram formed by the lines 3x−4y+1=0,3x−4y+3=0,4x−3y−1=0 and 4x−3y−2=0, is (A) 17squnits (B) 27squnits (C) 37squnits (D) 47squnits
View SolutionFind the area of the parallelogram formed by the lines
2x2+5xy+3y2=0and2x2+5xy+3y2+3x+4y+1=0View SolutionProve that the diagonals of the parallelogram formed by the four lines 3x+y=0,3y+x=0,3x+y=4,3y+x=4 are at right angles.
View SolutionThe perimeter of a parallelogram whose sides are represented by the lines x+2y+3=0,
3x+4y−5=0,2x+4y+5=0and3x+4y−10=0 is equal toView SolutionThe area bounded by the curve y2=4x and the line 2x−3y+4=0 is
View SolutionFind the co-ordinates of the point of intersection of the straight lines
2x−3y−7=0,3x−4y−13=0View SolutionDetermine the nature of the quadrilateral formed by four lines 3x+4y−5=0,4x−3y−5=0;3x+4y−5=0and4x−3y+5=0 Find the equation of the circle insc quadrilateral inscribed and circumscribing this quadrilateral.
View Solution30. Radical centre of circles drawn on the sides as a diameter of triangle formed by the lines the 3x−4y+6=0, x−y+2=0 and 4x+3y−17=0 is
View SolutionFind the values of the parameter a so that the point (a, 2) is an interior point of the triangle formed by the lines x+y-4=0, 3x-7y-8=0and 4x-y-31 = 0.
View Solution

