Question

Prove that the diagonals of a square are equal.

Explanation

To prove that the diagonals of a square are equal, we will follow these steps:

Step 1: Define the Square
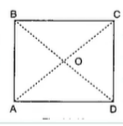
Let’s consider a square ABCD. The vertices of the square are A, B, C, and D, arranged in a clockwise manner.

Step 2: Identify the Diagonals
The diagonals of the square are AC and BD. We need to prove that AC = BD.

Step 3: Consider Two Triangles
We will consider two triangles: triangle ACD and triangle BCD.

Step 4: Identify the Sides of the Triangles
- In triangle ACD:
- Side AD = Side BC (since opposite sides of a square are equal)
- Side CD = Side CD (common side)

- In triangle BCD:
- Side BD = Side AC (the diagonals we are trying to prove equal)
- Side CD = Side CD (common side)

Step 5: Identify the Angles
- Angle ADC = Angle BDC = 90 degrees (since all angles in a square are right angles).

Step 6: Apply the Criteria for Congruence
Now we have:
1. AD = BC (from step 4)
2. CD = CD (common side)
3. Angle ADC = Angle BDC = 90 degrees (from step 5)

By the criteria of congruence (specifically the RHS criterion: Right angle-Hypotenuse-Side), we can conclude that triangle ACD is congruent to triangle BCD.

Step 7: Conclude the Proof
Since triangle ACD is congruent to triangle BCD, it follows that the corresponding parts of congruent triangles are equal. Therefore, we have:
AC = BD.

Thus, we have proved that the diagonals of the square are equal.

Final Statement
Hence, the diagonals AC and BD of square ABCD are equal.

---