Prove that the equation $2 sin x = | x | + a$ has no solution for $a \in (\frac{3 \sqrt{3} - π}{3}, \infty)$ .

Video Solution

Text Solution

Verified by Experts

$sin x = \frac{1}{2} | x | + \frac{a}{2}$
Draw the graphs of $y = 2 sin x and y = | x |$ .

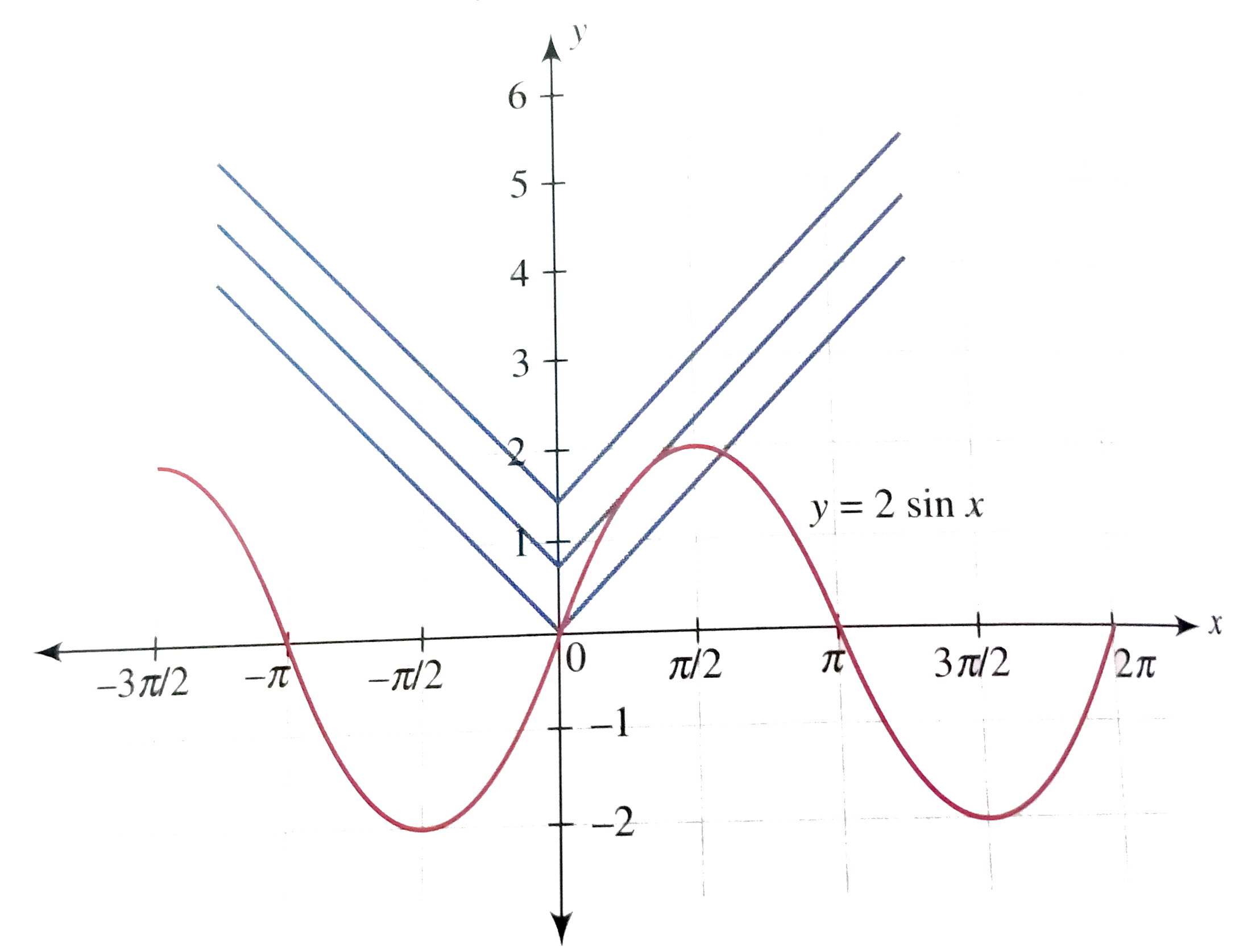
The equation $2 sin x = | x | + a$ will have a solution so long as the line $y = | x | + a$ intersects or at least touches the curve $y = 2 sin x$ . When the graphs touch, we have
$\frac{d y}{d x} = 2 cos x = 1, \Rightarrow x = \frac{π}{3}$
Hence for no solution,
$\frac{π}{3} + a > 2 sin \frac{π}{3}$
$\Rightarrow a > \frac{3 \sqrt{3} - π}{3}$

Updated on:21/07/2023