Prove that the perimeter of a right-angled triangle of given hypotenuse is maximum when the triangle is isosceles
Video Solution
Text Solution
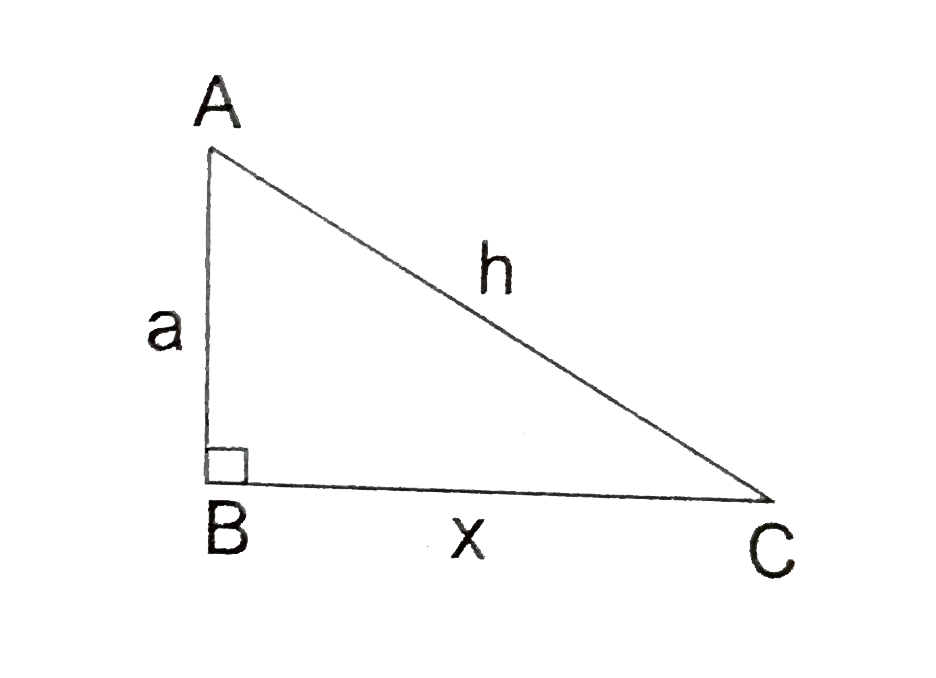
Let ABC be the right triangle with given hypotenuse h
Let, base BC = x and altitude BA=a
Then, h2=x2+a2⇒a=√h2−x2
∴P=a+x+h⇒P=√(h2−x2)+x+h
So, dPdx=−x√h2−x2+1andd2Pdx2=−h2(h2−x2)3/2
Now, dPdx=0⇒x=h√2
And for x=h√2,d2Pdx2=−23/2h<0
∴ P is maximum when x=h√2anda=h√2 i.e., when x = a
|
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11G
Explore 32 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11H
Explore 30 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11E
Explore 22 Videos
- ADJOINT AND INVERSE OF A MATRIXBook:RS AGGARWALChapter:ADJOINT AND INVERSE OF A MATRIXExercise:Exercise 7
Explore 37 Videos
- AREA OF BOUNDED REGIONS Book:RS AGGARWALChapter:AREA OF BOUNDED REGIONS Exercise:Exercise 17
Explore 39 Videos
Similar Questions
Knowledge Check
The maximum area of a right angled triangle with hypotenuse h is :
Ah22√2Bh22Ch2√2Dh24The perimeter of a right angled triangle is 24 cm. If its hypotenuse is 10 cm then area of this triangle is
A24 cm2B10 cm2C12 cm2D48 cm2The perimeter of a right angled triangle is 12 cm . The hypotenuse is 5 cm , then the area of the triangle is
A8cm2B10cm2C6cm2DNone of these
The maximum area of a right angled triangle with hypotenuse h is
View SolutionThe perimeter of a right angled triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
View SolutionThe perimeter of a right angled triangle is 60 cm. Its hypotenuse is 26 cm. The area of the triangle is
View SolutionThe perimeter of a right angled triangle is 12 cm . The hypotenuse is 5 cm , then the area of the triangle is
View SolutionThe perimeter of an isosceles right triangle is 2p, its area is
View Solution