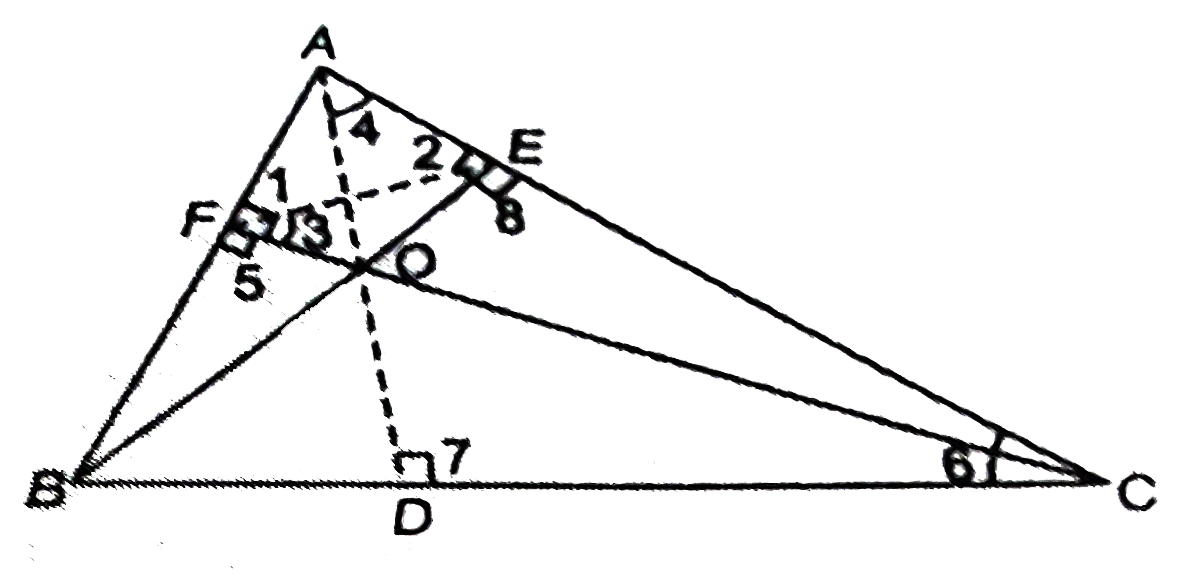
Prove that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
Given : ABC be a triangle in which BE and CF are perpendiculars drawn from B and C to the opposite sides AC and AB respectively .
To Prove : All the perpendicualar are concurrent i.e., pass through the same point.
Construction : join AO and produce, where it meets BC at D.
Proof : we have taken BE and CF as perpendiculars intersecting each other at O. if we prove that AOD⊥BC, it means all the three perpendicualars will pass through O.
Now, ∠1=∠2 (each 90∘)
∴∠1+∠2=90∘+90∘=180∘
∴□AEOF is a cyclic quadrilateral.
∴∠3=∠4 (angles of same segment are equal)....(1)
Now, since anl≥5=∠8 (each 90∘)
But these are the angles subtended by line segmetn joining two points on the same side of the line.
So, B,F,E,C are concyclic.
i.e., square BFEC is cyclic.
∴(∠5+∠3)+∠6=180∘ (sum of opposite angles of a cyclic qluadrilateral)
⇒90∘+∠4+∠6=180∘ [form (1)]
⇒∠4+∠6=90∘
Now, in ΔADC,
∠7+∠4+∠6=180∘
⇒∠7+90∘=180∘ (angle sum property)
∴∠7=90∘
It means line joining AO to D is perpendicular to BC.
Hence, all the perpendicular pass through the same point, i.e., they are concurrent.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
If p1,p2,p3 are respectively the perpendiculars from the vertices of a triangle to the opposite sides , then cosAp1+cosBp2+cosCp3 is equal to
A1/rB1/RC1/!Dnone of these
If ABC is an isosceles triangle with AB=AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionAltitudes the perpendiculars drawn from the vertices of a triangle to the opposite side are known as the altitudes of the triangle.
View SolutionThe coordinates of the feet of the perpendiculars from the vertices of a triangle on the opposite sides are (20, 25), (8, 16) and (8, 9). If the orthocentre of the triangle is (h, k) then k/h is equal to.
Note : The triangle joining the feel of the perpendiculars from the vertices of a trangle on the opposite sides is called the PEDAL TRIANGLE of the triangle.
View SolutionIf p1,p2 and p3 and are respectively the perpendiculars from the vertices of a triangle to the opposite sides, prove that : 1p1+1p2+1p3=1r.
View SolutionIf p1,p2,p3 are respectively the perpendicular from the vertices of a triangle to the opposite sides , then find the value of p1p2p3
View SolutionIf p1,p2,p3 are respectively the perpendicular from the vertices of a triangle to the opposite sides, then find the value of p1p2p3.
View SolutionIf p2,p2,p3 are the perpendiculars from the vertices of a triangle to the opposite sides, then prove that
p1p2p3=a2b2c28R3
View Solution
