Prove that volume of a parallelopiped with coterminal edges as ¯a,¯b,¯c is [¯a,¯b,¯c]. Hence find the volume of the parallelopiped with coterminal edges ˆi+ˆj,ˆj+ˆkandˆk+ˆi.
Video Solution
Text Solution
Let −−→OA,−−→OBand−−→OC represent the coterminus edges ¯a,¯band¯c respectively of the parallelo-piped. Draw segment AN perpendicular to the plane of ¯band¯c. Let ϕ be the angle between ¯band¯c and ϕ be the angle between the line AN and ¯a.
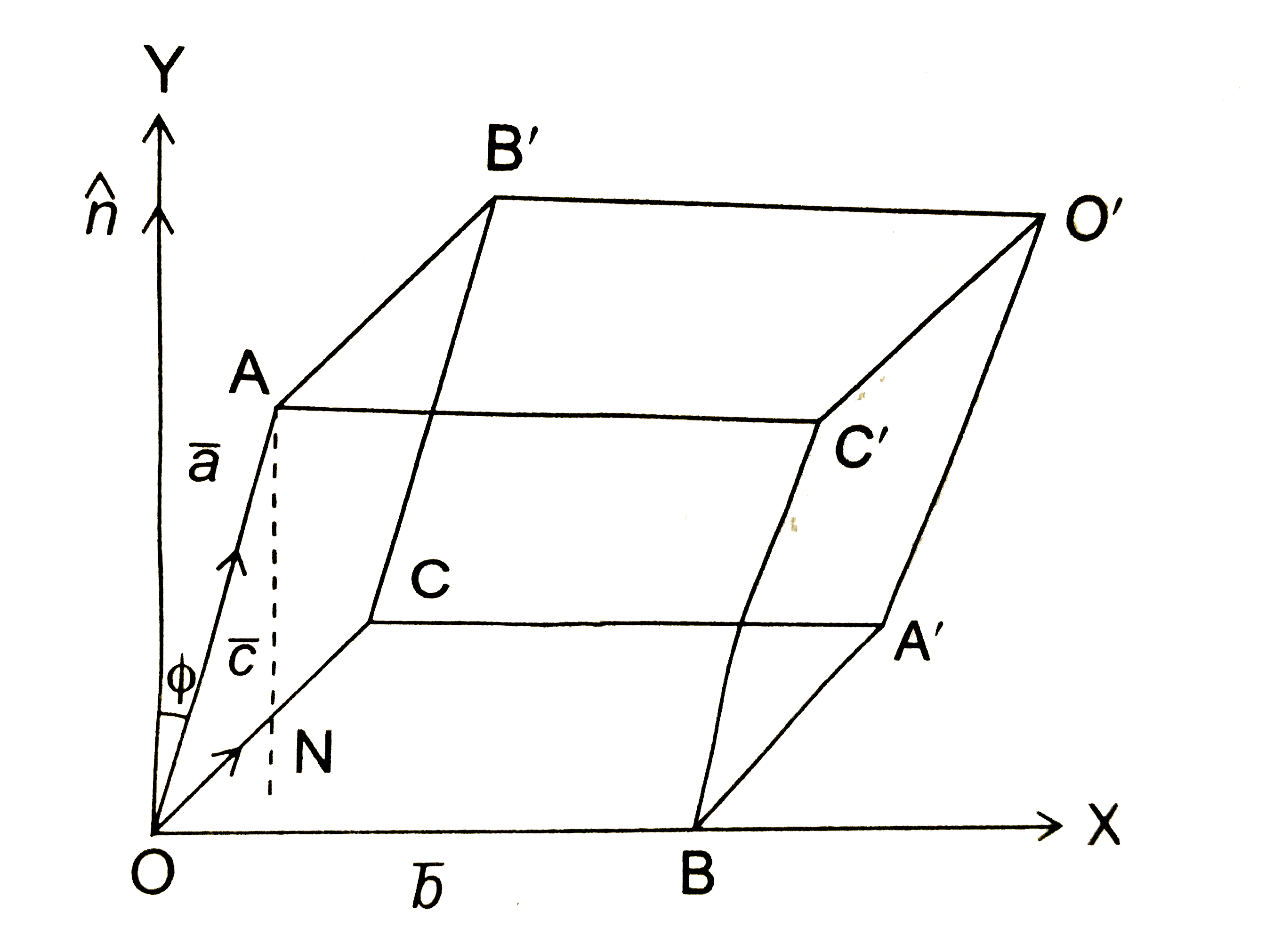
∴ANOA=cosϕ⇒AN=OAcosϕ=acosϕ ...(i)
If ˆn is the unit vector perpendicular to the plane of ¯band¯c, then the angle between ¯aandˆn is also ϕ.
∴ Volume of the parallelopiped
= Area of parallelogram (OBA'C×AN)
=bcsinθ×acosϕ [Using (i)]
=a(bcsinθ)cosϕ ...(ii)
Now, let us consider the scalar triple product
[¯a¯b¯c]=¯a.(¯bׯc)
¯bׯc=(bcsinθ)ˆn
∴ ∣∣¯bׯc∣∣=bcsinθ
∴ [¯a¯b¯c]=¯a.(¯bׯc)
|¯a|.∣∣¯bׯc∣∣cosϕ ...(iii)
From equations (ii) and (iii).
Volume of the parallelopiped =[¯a¯b¯c] ltBrgt Given ¯a=ˆi+ˆj,¯b=ˆj+ˆkand¯c=ˆk+ˆi
∴ [¯a¯b¯c]=⎡⎢⎣110011101⎤⎥⎦
=1(1−0)−1(0−1)+0(0−1)
=1+1+0=2
∴ The volume of the parallelopiped = 2 cubic units.
|
Topper's Solved these Questions
- OCTOBER 2014BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2014EXERCISE - SECTION - II
19 Videos
- MARCH 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2019EXERCISE - SECTION-D
13 Videos
- OCTOBER 2015BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2015EXERCISE - SECTION -II
20 Videos
Similar Questions
Prove that the volume of the parallelopiped with coterminus edges as ¯a,¯b,¯c is [¯a,¯b,¯c] and hence find the volume of the parallelopiped with its coterminus edges ˆi+5ˆj−4ˆk,5ˆi+7ˆj+5ˆk and 4ˆi+5ˆj−2ˆk.
View SolutionFind the volume tetrahedron whose coterminus edges are 7ˆi+ˆk,2ˆi+5ˆj−3ˆkand4ˆi+3ˆj+ˆk.
View Solution
Knowledge Check
The volume of the tetrahedron whose co-terminous edges are ˆj+ˆk,ˆk+ˆi,ˆi+ˆj is
A16cu. UnitsB13cu. UnitsC12cu. UnitsD23cu. UnitsThe volume of the paralleloP1ped with co-terminous edges given by the vectors ˆj+ˆk,ˆi+3ˆk,ˆi+ˆj is
A3cu. UnitsB4cu. UnitsC1cu. unitsD2cu. UnitsIf the volume of the tetrahedron formed by the coterminus edges ¯a,¯band¯c is 4, then the volume of the parallelopiped formed by the coterminous edges ¯aׯb,¯bׯcand¯cׯa is
A144B16C48D576
Prove that [ˆiˆjˆk]=1,and[ˆiˆkˆj]=−1.
View SolutionFind the angle between ˆi+ˆj+ˆk and ˆi+ˆj−ˆk.
View SolutionFind the volume of the parallelopiped whose coterminus edges are given by vectors 2ˆi+3ˆj−4ˆk,5ˆi+7ˆj+5ˆkand4ˆi+5ˆj−2ˆk.
View SolutionThe volume of the parallelepiped whose edges are −−→OA=2ˆi−3ˆj,−−→OB=ˆi+ˆj−ˆk,−−→OC=3ˆi−ˆk is
View SolutionThe volume of the paralleloP1ped with co-terminous edges given by the vectors 3ˆi+5ˆj,4ˆi+2ˆj−3ˆk,3ˆi+ˆj+4ˆk is
View Solution
